שתי התכונות האלה (חוסר הטיה ושונות קטנה יחסית) של האומדים מתקיימות רק אם מתקיימות 5 הנחות. ההנחות הללו נקראות ההנחות הקלאסיות:
- המשתנים המסבירים אינם משתנים מקריים.
- בכל אחת מהתצפיות התוחלת של היא 0.
- בכל אחת מהתצפיות, השונות של זהה (מסומנת ).
- אין מתאם בין -ים של תצפיות שונות.
- בכל אחת מהתצפיות התפלגות היא נורמלית.
הערה: הנחה (5) איננה הכרחית לקיום חוסר ההטיה והשונות הקטנה של האומדים, אך בלעדיה לא היינו יכולים לצייר את התרשימים שלעיל שהם בצורת העקום הנורמלי.
המשתנים המסבירים אינם משתנים מקריים (הנחה 1)
בניסוי על ערוגות החצילים שתואר בפרקים הקודמים, כמות המים שבה הושקתה כל ערוגה (X) לא היתה משתנה מקרי, כיוון שהיה ידוע מראש כמה מים מקבלת כל ערוגה. החוקר היה יכול לעשות ניסוי אחר: במקום לרכז את כל הערוגות בחממות הניסויים שלו ולהשקות אותן כרצונו, הוא היה יכול לפזר את ערוגותיו ב- 20 מקומות שונים בארץ, מדן ועד אילת, ליד כל ערוגה להניח מד גשם, ולהניח לחצילים לצמוח ממי הגשמים בלבד. גם בניסוי הזה ניתן לדעת את כמות המים שקיבלה כל ערוגה ואת משקל החצילים וכך לאמוד את הקשר שבין כמות המים למשקל החצילים, אבל בניסוי זה כמות המים (המשתנה המסביר) היא משתנה מקרי, כי כמות הגשם איננה ידועה מראש.
בכל אחת מהתצפיות התפלגות היא נורמלית (הנחה 5); בכל אחת מהתצפיות התוחלת של היא 0 (הנחה 2); בכל אחת מהתצפיות, השונות של זהה (הנחה 3).
ההתפלגות של הסטיות האקראיות מהקו ( ) זהה בכל תצפית ותצפית, והיא מקבלת את הצורה של העקום הנורמלי ("הפעמון"), כאשר במרכז הפעמון נמצא הערך 0.
באופן זה הערך של המשתנה המוסבר מתפלג בצורה של העקום, כשהסיכוי ש- יהיה שלילי הוא 50%, והסיכוי ש- יהיה חיובי גם הוא 50%.
הפיזור אף הוא זהה בין התצפיות.
הוא יכול להיות קטן כמו בתרשים הבא:
כאשר הפיזור של קטן, אזי בכל אחת מהתצפיות מקבל בסיכוי גבוה ערכים קרובים ל- 0. במקרה זה התצפיות קרובות לקו הרגרסיה.
הפיזור יכול להיות גם גדול כמו בתרשים הבא:
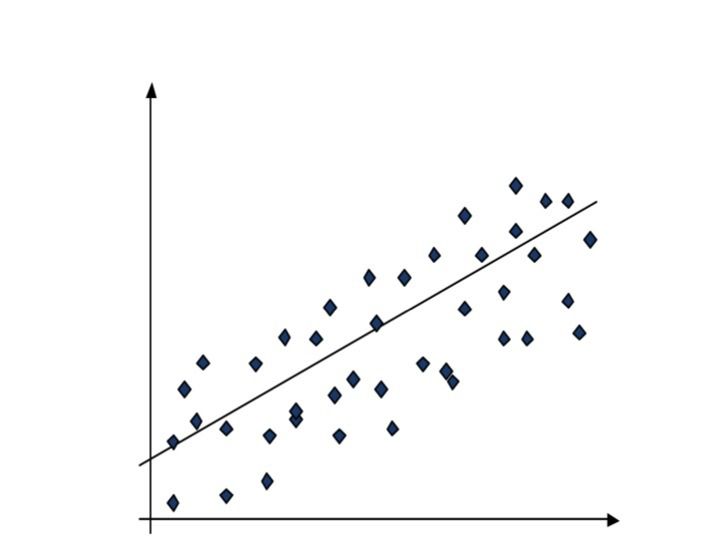
כאשר הפיזור של גדול, אזי בכל אחת מהתצפיות יכול לקבל בסיכוי גבוה ערכים רחוקים מ- 0. במקרה זה יהיו תצפיות רחוקות מקו הרגרסיה.
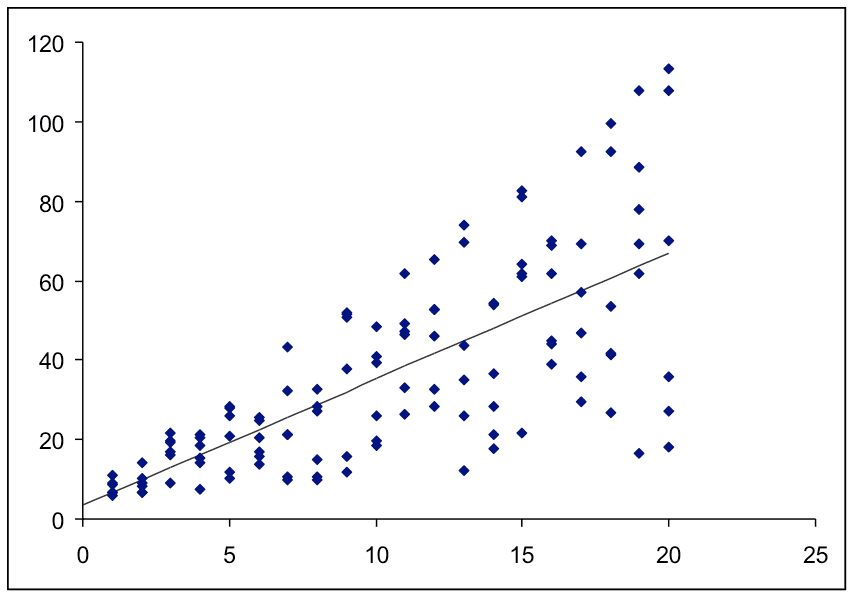
התרשים הבא ממחיש מצב שבו השונות איננה קבועה (הפרה של הנחה 3):
יש אזור שבו השונות קטנה (התצפיות מפוזרות בקרבת הקו) ויש אזור שבו השונות גדולה (התצפיות רחוקות מהקו).
אין מתאם בין -ים של תצפיות שונות (הנחה 4)
להנחה זו יש משמעות עבור מדגמים שבהם ניתן לסדר את התצפיות, בעיקר נתונים המסודרים לפי הזמנים שאליהם הם שייכים. למשל, אם נרצה לבדוק איך מתפתח התוצר הלאומי בישראל כפונקציה של הזמן, נוכל לאסוף נתונים המסודרים לפי שנים.
להלן נתונים של הלשכה המרכזית לסטטיסטיקה על התוצר המקומי הגולמי בישראל משנת 1950 ועד שנת 1995 (במליוני ש"ח במחירי 1995).
| שנה | מקומי גולמי תוצר | שנה | מקומי גולמי תוצר | |
| 1950 | 12,901 | 1973 | 108,723 | |
| 1951 | 16,788 | 1974 | 114,722 | |
| 1952 | 17,527 | 1975 | 119,116 | |
| 1953 | 17,273 | 1976 | 120,996 | |
| 1954 | 20,624 | 1977 | 123,446 | |
| 1955 | 23,439 | 1978 | 128,517 | |
| 1956 | 25,529 | 1979 | 134,588 | |
| 1957 | 27,786 | 1980 | 139,378 | |
| 1958 | 29,821 | 1981 | 145,961 | |
| 1959 | 33,624 | 1982 | 148,040 | |
| 1960 | 35,844 | 1983 | 151,868 | |
| 1961 | 39,750 | 1984 | 155,225 | |
| 1962 | 43,720 | 1985 | 162,134 | |
| 1963 | 48,327 | 1986 | 167,891 | |
| 1964 | 53,122 | 1987 | 178,209 | |
| 1965 | 57,383 | 1988 | 184,560 | |
| 1966 | 57,957 | 1989 | 187,180 | |
| 1967 | 59,293 | 1990 | 199,595 | |
| 1968 | 68,408 | 1991 | 211,760 | |
| 1969 | 77,108 | 1992 | 226,911 | |
| 1970 | 83,020 | 1993 | 235,468 | |
| 1971 | 92,373 | 1994 | 251,977 | |
| 1972 | 103,677 | 1995 | 268,442 |
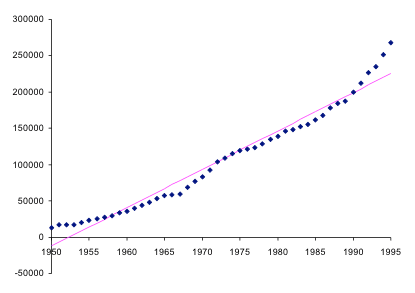
הנתונים שבטבלה מוצגים בגרף שלהלן (נקודות בכחול), כמו כן מופיע (בורוד) קו הרגרסיה המתאים. כמו בכל קו רגרסיה, חלק מהתצפיות מופיעות מעל לקו (ה- חיובי) וחלק מתחת לקו (ה- שלילי). אך בגרף שלהלן נקודות שמעל לקו נמצאות בסמיכות זו לזו ונקודות שמתחת לקו נמצאות בסמיכות זו לזו. כלומר, אם של תצפית מסויימת הוא חיובי, אזי ה- של התצפית הסמוכה יטה להיות חיובי אף הוא, ואם של תצפית מסויימת הוא שלילי, אזי ה- של התצפית הסמוכה יטה להיות שלילי אף הוא. במקרה כזה אנו אומרים כי יש מתאם בין ה- -ים, והנחה (4) לא מתקיימת.