עד כה כללנו במודל קיינס 3 מרכיבים: צריכה פרטית C + השקעה I + הוצאות ממשלה G.
עכשיו נשלב במודל עוד 2 מרכיבים: מיסים וסחר בינ”ל. סחר בינ”ל מאפיין משק פתוח.
סחר בינ”ל ייצוא נטו. סימול [N.Ex]
ייצוא
הייצוא נובע מהביקוש של זרים לרכישת מוצרים מהמדינה.
ייבוא
הייבוא נובע מביקוש מקומי לרכישת מוצרים מחו”ל.
השפעת הייצוא נטו על התמ”ג
במשק סגור כל המוצרים המיוצרים במדינה מהווים את התמ”ג שלה.
אם לדוגמה במשק קטן א' שהוא משק סגור מייצרים רק 1000 לחמים במחיר של 10 ש”ח ללחם, אזי התמ”ג בה מסתכם ב- 10,000 ש”ח. משק סגור מייצר את כל חומרי הגלם בעצמו.
אם המשק נפתח לסחר בינ”ל ולצורך ייצור הלחמים הוא ייבא קמח בשווי של 2000 ש”ח ומנגד הוא ייצא 300 לחמים לחו”ל, אזי ערך המוצרים שהמדינה תייצר יגיע ל- 13,000 ש”ח (= 1300 לחמים * 10 ש”ח).
תושבי חו”ל תרמו לערך המוצרים 2000 ש”ח (הם עמלו בייצור הקמח).
התושבים המקומיים תרמו לערך המוצרים את היתרה, 100,000 ש”ח. תרומת המקומיים היא התמ”ג שנסמלו Y.
ניתן להציג זאת כך:
| סך ערך המוצרים | |||||
| ייבוא | ייצוא | ביקוש מקומי | |||
| 2000 ש”ח | – | (10 ש”ח * 300 לחמים) | + | (10 ש”ח * 1000 לחמים) | Y= |
או כך:
| ייצוא נטו | ביקוש מקומי |
| [2000-(300*10)] | + (1000*10) |
והמסקנות
- גידול בייצוא נטו תורם לגידול בתמ”ג.
- הייצוא נטו יכול לגדול כתוצאה מגידול בייצוא ו/או קיטון בייבוא או בשעה ששניהם גדלים, אך הייצוא גדל יותר.
מאפייני עקומת ההוצאות המצרפיות לייצוא נטו N.Ex
לצורך הפשטות נניח את ההנחות הבאות לגבי הייצוא והייבוא.
ייצוא
הייצוא הוא סכום קבוע שאינו מושפע מההכנסות.
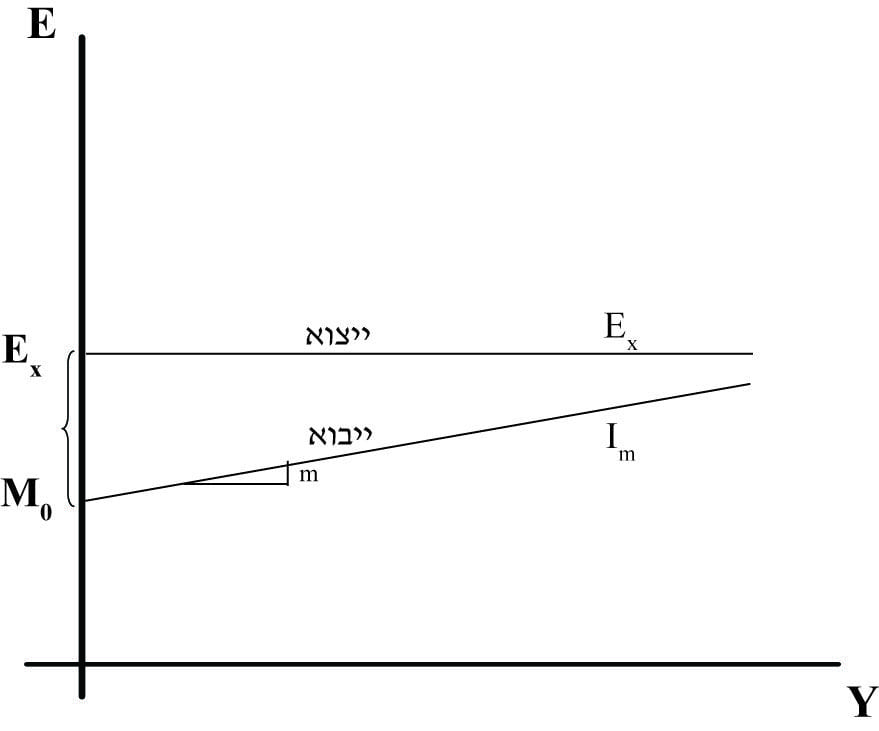
את פונקציית הייצוא נסמל Ex. צורתה קו אופקי בגובה Ex0 כפי שמוצג בתרשים 700.
תרשים 700
ייבוא
תרשים 701
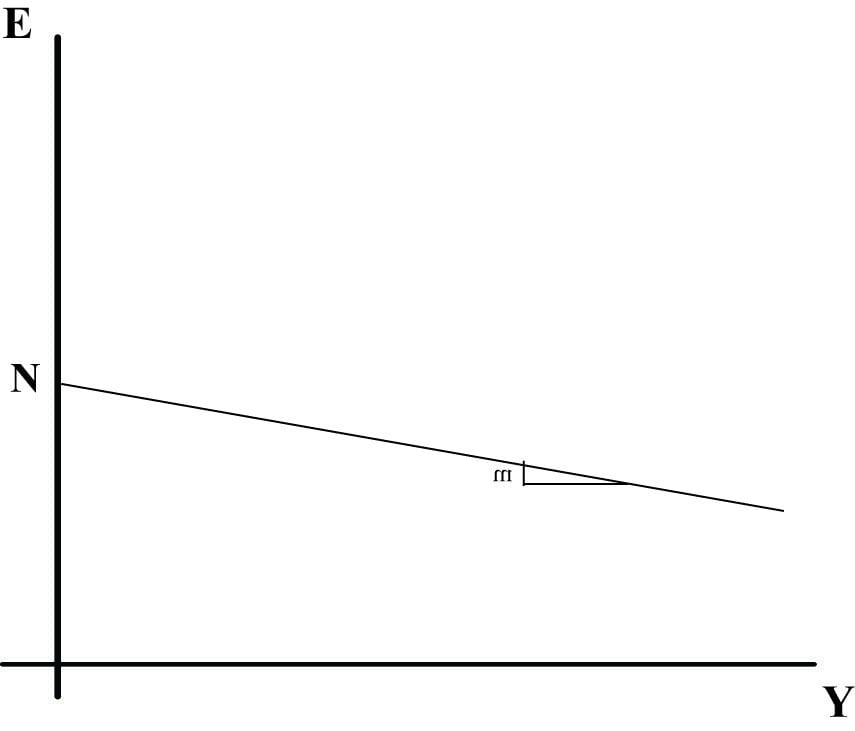
הפער בין הייצור לייבוא הוא פונקציה לינארית שצורתה: `[Ex_0-M_0]-mY=Ex_0-[M_0+mY]`
כשנוסיף את המרכיב של N.Ex ל- 3 המרכיבים האחרים C, I ו- G, השיפוע של m שהוא שלילי, ימתן את השיפוע החיובי של C כך שהשיפוע של עקומת ההוצאה המצרפית יהיה: [m-c]. אם c=0.8 ו- m=0.1- השיפוע יהיה 0.7.
תוואי פונקציית ההוצאה המצרפית הכוללת את N.Ex
פונקציית ההוצאה המצרפית היא סכום המרכיבים שלה:
`E=G_0+I_0+[C_0+cY]+[N_0-mY]`
אם נפתח את הסוגריים ונשנה את סדר האיברים נקבל:
`E=[G_0+I_0+C_0+N_0]+(c-m)Y`
נסמן ב- E0 את האיבר G0+I0+C0+N0 וצורת הפונקציה תהיה `[E_0+(c-m)Y]`.
כאשר m=0 שיפוע הפונקציה זהה לשיפוע שיהיה ללא מרכיב ה- N.Ex.
חישוב המכפיל כאשר מתווסף N.Ex
המכפיל הוא `1/(1-(c-m)` או `1/(1-c+m`
(m = שיפוע קו הייבוא \ נטיה שולית לייבא).
וההסבר: במקום המפגש של קו 450 ופונקציית ההוצאה המצרפית מתקיימים 2 תנאים:
- `E_F=Y_F`
- `E_F=E_0+(c-m)*Y_F`
אם נציב במשוואה (2) EF במקום YF ונשנה את מיקום האיברים, נקבל: `E_F=E_0/(1-(c-m)`.
אם נחלק ב-E0 את 2 צדי המשוואה נקבל:
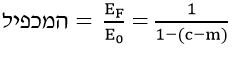
עוד נשוב ונרחיב לגבי הגורמים שמשפיעים על הגדלה או הקטנה של N.Ex.