הקדמה
- המס שהממשלה גובה מיועד בעיקר ל-2 מטרות:
a. לממן את פעילות הממשלה
b. תשלומי העזרה לשכבות נזקקות כדוגמת קיצבה לזקנים נכים סעד וכיוב'. - אנו מניחים שהמס נגבה ב-2 מסלולים בלבד.
- מסלול 1 – סיכום קבוע כלשהו שאינו מותנה בגובה ההכנסה הוא משולם גם כאשר ההכנסה היא אפס. נסמלו T0.
- מסלול 2 – מס בשיעור אחיד על ההכנסה למשל,30% על כל דולר של הכנסה. נסמלו: t .
עדכון פונקציית הצריכה
כאשר קיים מס הנטייה השולית לצרוך שסימולה C מתייחסת להכנסה הפנויה (ההכנסה לאחר מס) ולא להכנסה לפני תשלום המס (Y).
כזכור, כאשר אין מס, פונקציית הצריכה היא `C=C_0+cY` .
אך כאשר מוטל מס, במקום Y נציב בפונקציית הצריכה את ההכנסה הפנויה, שסימולה: DI.
וצורת פונקציית הצריכה משתנה ל: `C=C_0+C*DI` [שוויון 1].
כאשר תשלום המס נעשה בהתאם להנחה שלנו לגבי 2 המסלולים ההכנסה הפנויה היא: `DI=Y-T_0-ty` .
אם נציב בשיוויון 1 `(C=C_0+C*DI)` במקום DI את החלופה שלו `(DI=Y-T_0-ty)` , נקבל את שיוויון 2: `C=C_0+c[Y-T_0-ty]` [שוויון 2]
כשנפתח סוגריים ונארגן את האברים מחדש נקבל פונקציה ליניארית שצורתה:
`C=[C_0-CT_0]-C(1-t)*Y`
השיפוע: `C(1-t)` סכום קבוע: `[C_0-CT_0]`
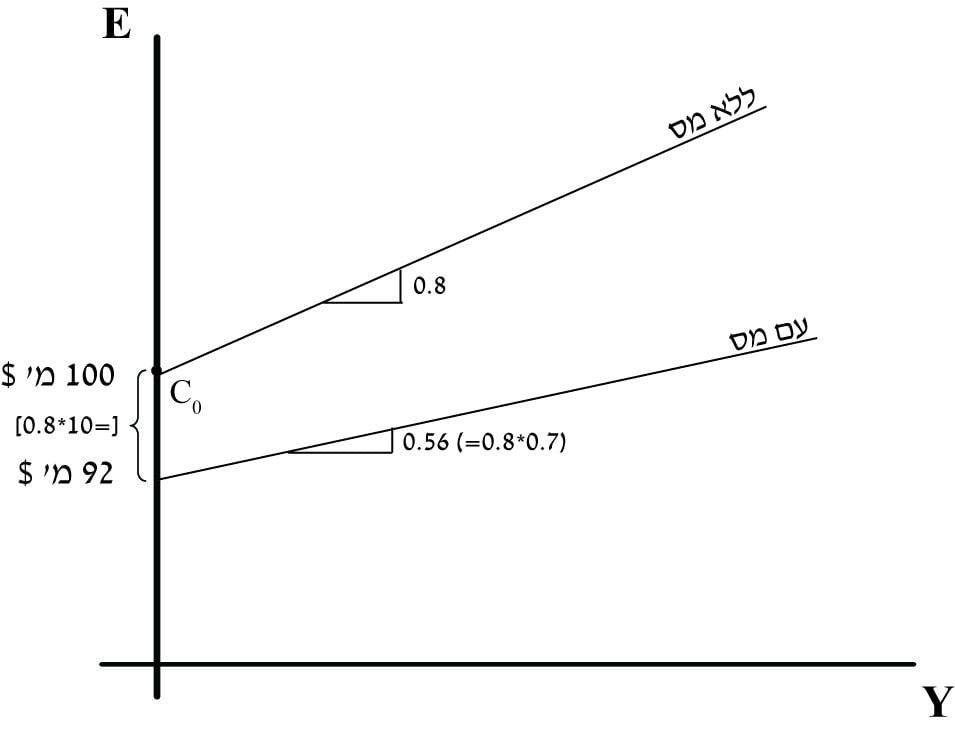
בתרשים 703 מתוות 2 פונקציות צריכה.
- הפונקצייה העליונה מתייחסת למצב שבו לא מוטל מס.
- הפונקצייה התחתונה מתייחסת למצב שבו מוטל מס.
הנתונים שעליהם הפונקציות מבוססות הן כדלקמן:
`C_0` – 100 מ'$.
`T_0` – 10 מ'$.
c – 0.8
t – 0.3
תרשים 703
פרשנות
שיפוע הפונקציות
- כאשר לא מוטל מסף כל תוספת הכנסה של 1$, מגדילה את הצריכה ב-`0.8$(=c*1$)`
- כאשר מוטל מס, כל תוספת הכנסה של 1$, מגדילה את הצריכה ב-`(c*(1-t)$=) $0.56`
נקודת החיתוך עם ציר ה-Y , כאשר מוטל מס
כאשר ההכנסות הן אפס, סכום המס האפקטיבי הוא T0$. כאשר ההכנסות הן 0 , `0=t*y` . המס מקטין את ההכנסה הפנויה ב-T0$, במצב זה הכנסה הפנויה היא `(0-=)-`.
כלומר, הכנסה פנויה שלילית.
אך כל ירידה של 1$ בהכנסה הפנויה גם כשהיא שלילית מקטינה את הצריכה בשעור הנטיה השולית לצרוך (c) כלומר ב-0.8$. כך שירידה של T0$ בהכנסה הפנויה מקטינה את הצריכה ב- `c*T_0$` .
פונקציית ההוצאות המצרפיות כאשר מוטל מס
הפונקציה זהה לפונקציית ההוצאות המצרפיות ללא מס עם 2 תיקונים קלים:
- במקום C0 נציב `C_0-c*T_0` .
- במקום c נציב `c(1-t)` .
|
לפני |
– m)Y |
C |
+ |
[G0+I0+C0+N0] |
= E |
| E0 `darr` | |||||
|
אחרי |
m]Y – |
(C(1-t] |
+ |
[+G0+I0+N0+(C0-cT0)] |
= E |
אם נסמל את התוצאה בסוגריים השמאליים ב- E0 צורת הפונקצייה תשתנה ל: E=E0+[c(1-t)-m]Y .
איך זוכרים את הפונקציות
אי אפשר לזכור, וגם אין צורך לזכור. מה שחשוב לזכור זה:
- שפונקציית ההוצאות המצרפיות, עם או בלי מס, היא קו עולה (שיפוע חיובי).
- שתוספת מס, מקטינה את שיפוע הפונקציה ומורידה את נקודת החיתוך.