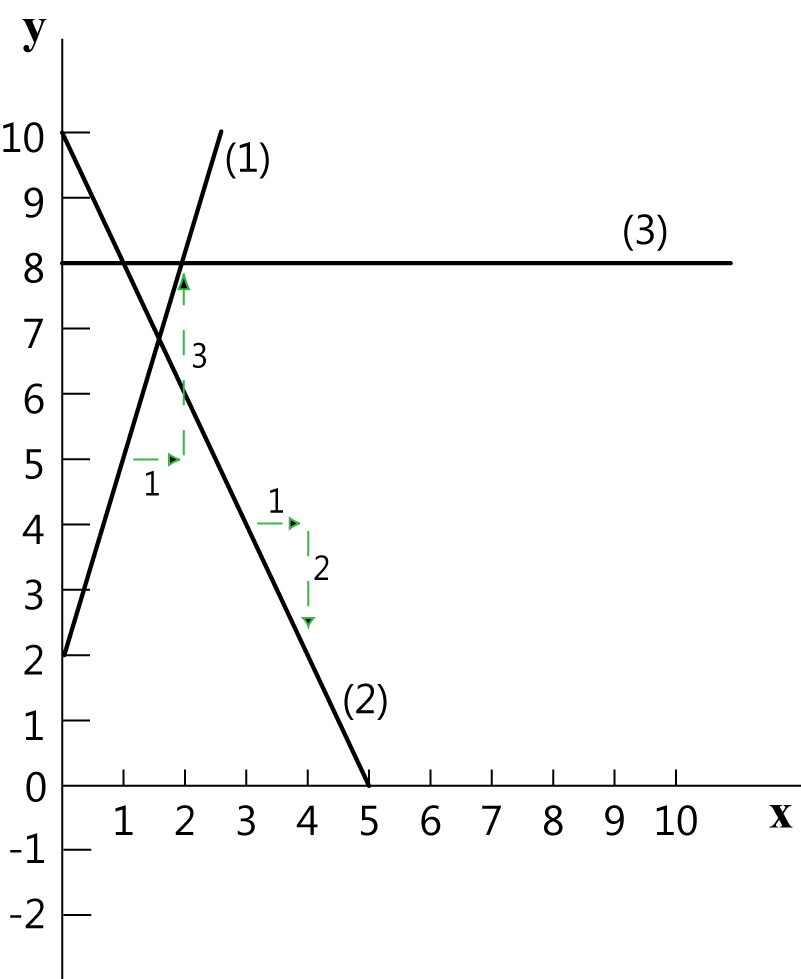2 תכונות מאפיינות כל קו ישר:
- ערך ה-y של הנקודה שבה הקו חותך את ציר ה- y (בהתנסחות מתמטית: ערך ה- y בנקודת החיתוך).
- השיפוע שלו.
ערך ה- y בנקודת החיתוך
ערך ה- y בנקודת החיתוך הוא תמיד המספר שמייצג את הפרמטר b (בנוסחה y=ax+b).
זאת מהסיבה הפשוטה שהחיתוך מתבצע כאשר x=0 ואז 0=x·a ובנוסחה נותר רק b.
[y=ax+b] . (0 = ax) מכאן שבנקודת החיתוך y = b
שיפוע הקו
שיפוע הקו מוגדר כמספר היחידות שמשתנות בתוצאה – כתוצאה מתוספת של 1 יחידה ב- x. השיפוע מוצג כמספר כלשהו (כמספר היחידות המשתנות). השיפוע יכול להיות חיובי, שלילי או 0.
שיפוע חיובי
כאשר תוספת של 1 יחידה ב- x גורמת, לדוגמה, לתוספת של 3 יחידות ב- y כמו בנוסחה `y=3x+2` , השיפוע הוא 3 והוא חיובי. שיפוע חיובי מאופיין כקו עולה, כדוגמת התרשים הקודם או כדוגמת קו (1) בתרשים הבא.
שיפוע שלילי
כאשר תוספת של 1 יחידה ב- x, גורמת לגריעה של 2 יחידות ב- y, כמו לדוגמה בנוסחה `y=-2x+10` , השיפוע הוא 2- והוא שלילי. שיפוע שלילי מאופיין בקו יורד כדוגמת קו (2) בתרשים.
שיפוע 0
כאשר תוספת של 1 יחידה ב- x לא גורמת לשינוי במספר היחידות ב- y, השיפוע הוא 0. שיפוע 0 מאופיין כקו אופקי כדוגמת קו (3) בתרשים.
בקו ישר השיפוע אחיד לאורך כל הקו
בקו ישר, השיפוע לא משתנה לאורך הקו. בגין כל תוספת של 1 יחידה ב- x, יחול אותו שינוי במספר היחידות ב- y.
פרמטר a מציין את שיפוע הקו
המספר שמייצג את פרמטר a, נוקב בשיפוע הקו.
וההסבר: כל שינוי של 1 יחידה ב- x, מגדיל או מקטין את y בעוד a יחידות.
דוגמאות
בטבלה הבאה מוצגות בטור 1 שלוש נוסחאות של קווים ישרים ולצידן בטורים 2 ו- 3 מפורטים שני הפרמטרים a ו- b, המתלווים לכל נוסחה.
|
הנוסחה |
השיפוע (פרמטר a) |
ערך ה- y בנקודת החיתוך (פרמטר b) |
|
(1) |
(2) |
(3) |
|
`y=-2x+5` |
2- |
5 |
|
`y=0.3x-6` |
0.3 |
6- |
|
`y=-0.3x-6` |
0.3- |
6- |