הקדמה
נקודת קיצון מקומי – המשמעות
נקודת קיצון מקומי היא הנקודה הגבוהה ביותר או הנמוכה ביותר באזור שלה על מעטפת הפונקציה.
מיון נקודות קיצון – תזכורת
אנו מבחינים ב- 4 סוגים של נקודות קיצון:
- נקודת קיצון מקסימום מוחלט.
- נקודת קיצון מינימום מוחלט.
- נקודת קיצון מקסימום מקומי.
- נקודת קיצון מינימום מקומי.
ציון המיקום של נקודות הקיצון
את המיקום של נקודת קיצון מקובל לציין באמצעות נקודת ציון במישור הצירים, שנמצאת מתחת או מעל לנקודת הקיצון.
שימוש בנגזרת הראשונה
באמצעות הנגזרת הראשונה אנו מקבלים סדרת נקודות על המעטפת שנקרא להן: נקודות חשודות, שרק מתוכן תמצאנה, אם בכלל, נקודות קיצון.
שימוש בנגזרות השניות
באמצעות הנגזרות השניות, אנו יכולים לבחון מי מה”נקודות החשודות” הן נקודות קיצון ומאיזה סוג (מקסימלי, מינימלי, מוחלט, מקומי).
סימולים – השלמות
|
סימול |
משמעות |
פרשנות |
|
(f(x,5 |
תוצאות הפונקציה כאשר 5 = y |
זו הפונקציה של רצועת רוחב 5 |
|
(f(x,a |
a מציין נתון מספרי קבוע כלשהו |
זו הפונקציה של רצועת רוחב a |
|
(f(3,y |
תוצאות הפונקציה כאשר 3 = x |
זו הפונקציה של רצועת אורך 3 |
|
(f(a,y |
a מציין נתון מספרי קבוע כלשהו |
זו הפונקציה של רצועת אורך a |
|
(f(3,5 |
תוצאת הפונקציה בנקודת הציון (3,5) |
|
|
(f(a,b |
תוצאת הפונקציה בנקודת הציון (a,b) |
|
תנאים לקיומן של נקודות קיצון
על-מנת שנקודה בפונקציה תהיה נקודת קיצון, עליה לקיים את שני התנאים הבאים:
תנאי 1: בנקודת הקיצון, הנגזרת הראשונה לפי x, שווה ל-0 וגם הנגזרת הראשונה לפי y שווה ל- 0.
בשפת הסימולים: fx(x,y)=0
fy(x,y)=0
תנאי 2: fxx(x,y)·fyy(x,y) – [fxy(x,y)]2 > 0
כאשר fxx(x,y) < 0 או ש- fyy(x,y) < 0 מדובר בנקודת מקסימום.
כאשר fxx(x,y) > 0 או ש- fyy(x,y) > 0 מדובר בנקודת מינימום.
המחשה לכך שהתנאי הראשון בלבד לא תמיד מספיק
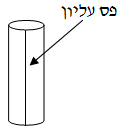
1. כאשר המעטפת היא בצורת חצי גליל עליון, אין לפונקציה נקודת קיצון, למרות העובדה שבכל נקודה לאורך הפס העליון בגליל, הנגזרת לפי x שווה אפס והנגזרת לפי y גם שווה לאפס. כלומר, אין נקודת קיצון למרות שתנאי 1 מתקיים.
2. מנגד, כאשר המעטפת היא בצורת חצי כדור עליון, יש לפונקציה נקודת קיצון שנמצאת בפסגת הכדור. בנקודת הקיצון: הנגזרת לפי x שווה 0 וגם הנגזרת לפי y שווה 0 ותנאי 1 מתקיים.
טכניקת מציאת נקודת קיצון ב- 4 מהלכים, בליווי דוגמה
הדוגמה מתייחסת לפונקציה f(x,y) = x2 – 6x + y2 – 8y + 30 .
נגזרות ראשונות
מהלך 1: גוזרים את הפונקציה פעם לפי x ופעם לפי y
והתוצאה:
נגזרת לפי x – fx(x,y)=2x-6
נגזרת לפי y – fy(x,y)=2y-8
מהלך 2: מוצאים את הערכים של x ו- y שמקיימים את השיוויון 0=2x-6 וכן 2y-8=0 (אם ישנם). את הערכים מוצאים בטכניקות אלגבריות.
הערכים הנ”ל, אם ישנם, הם נתוני נקודות הציון (x,y) שמתייחסות לנקודות על המעטפת, החשודות כנקודות קיצון.
התוצאה בדוגמה: ישנה רק נקודת ציון אחת. נתוניה: 3=x ו 4=y. סימול הנקודה (3,4).
סימול הפונקציה בנקודה זו הוא f(3,4).
נגזרות שניות
מהלך 3: מחשבים את תוצאות הנגזרות השניות, הדרושות לבדיקת תנאי 2 שהן:
|
תוצאות הנגזרות השניות |
פרשנות |
|
fxx(x,y)=2 |
השיפוע של כל רצועת רוחב בפונקציה המקורית עולה ב- 2 יח' מפסיעה לפסיעה. |
|
fyy(x,y)=2 |
השיפוע של כל רצועת אורך בפונקציה המקורית עולה ב- 2 יח' מפסיעה לפסיעה. |
|
fxy(x,y)=0 |
1. לאורך אותו קו אורך, פערי השיפוע מרצועת רוחב אחת לשנייה לא משתנים. לדוגמה: לאורך רצועת אורך 1 מציבים 1 = x בתוצאת הנגזרת הראשונה השיפוע קטן ב- 4, מרצועת רוחב לרצועת רוחב. לאורך רצועת אורך 5 השיפוע גדל ב-4, מרצועת רוחב לרצועת רוחב (הצבנו 5 = x בתוצאת הנגזרת). לאורך רצועת אורך 3 השיפוע משתנה ב- 0 מרצועת רוחב לרצועת רוחב (הצבנו 3 = x בתוצאת הנגזרת). 2. פערי השיפוע הולכים וגדלים ככל ש – x הולך וגדל. לדוגמה: כאשר x = 1, פער השיפועים בין רצועות הרוחב עומד על 4-. כאשר x = 5, הפער עולה ל- 4. כאשר x = 10, הפער עולה ל- 14. למעשה, עם כל “פסיעה” לאורך ציר ה- x, פערי השיפוע גדלים ב- 2. וההסבר, תוצאת הנגזרת שקיבלנו: , היא פונקציה של x שמייצגת קו ישר, ששיפועו 2. 3. y לא משפיע על התוצאה. |
מהלך 4: חישוב קיומו של תנאי 2 בנקודת הציון (3,4). התוצאה: [SIGN][SIGN][SIGN]
הערה: בדוגמא שלנו האיבר השלישי [fxy(x,y)]2 תמיד יהיה שווה לאפס ואין זה משנה אילו ערכים של x נציב בפונקציה. עם זאת, כמובן שיכולות להיות לנו פונקציות אחרות שגזירתן לפי הצורה[fxy(x,y)]2 תתן לנו תוצאה שונה מאפס.
המסקנה: תנאי 2 מתקיים ולפונקציה יש נקודת קיצון מעל נקודת ציון (3,4).