סטית תקן – מדד לפיזור - מיטב לימוד עצמי

התוחלת איננה מדד מספק כדי לתאר התפלגות. יתכן כי לשתי התפלגויות בעלות אופי שונה לגמרי תהיה בדיוק אותה תוחלת. דבר דומה ראינו בפרק על המדדים בהקשר של הממוצע.

נראה זאת באמצעות דוגמא. נתבונן בשתי ההתפלגויות הבאות:

התפלגות א':

הערך	ההסתברות
2	0.30
3	0.25
5	0.25
7	0.20
סה”כ	1.00

התפלגות ב':

הערך	ההסתברות
0	0.25
1	0.25
7	0.25
8	0.25
סה”כ	1.00

הערה: ההתפלגויות הנ”ל הן אינן תוצאות של שום ניסוי מציאותי מוכר, אבל נוכל להניח כי קיים ניסוי כזה. בשלב מתקדם זה של החומר, נוכל להתחיל לחשוב בצורה יותר מופשטת, ולא לנסות ולמצוא ניסוי מציאותי. אבל אם בכל זאת נתעקש נוכל לדמיין לנגד עינינו 2 סביבונים. על האחד כתובים (במקום נס-גדול-היה-פה) ארבעה מספרים 8,7,1,0 וכל אחד מהמספרים מתקבל בהסתברות שווה. סביבון זה מתאים להתפלגות ב'. על הסביבון השני כתובים המספרים 7,5,3,2. סביבון זה איננו סביבון “הוגן”, כלומר למספרים מסויימים יש נטיה להתקבל בסיכוי גבוה יותר מאשר מספרים אחרים. סביבון זה מתאים להתפלגות א'.

נחשב את התוחלת של שתי ההתפלגויות הנ”ל:

התפלגות א':

`4=7*0.2+5*0.25+3*0.25+2*0.3`

התפלגות ב':

`4=8*0.25+7*0.25+1*0.25+0*0.25`

התוחלת של שתי ההתפלגויות היא זהה, 4.

אך האם שתי ההתפלגויות זהות?

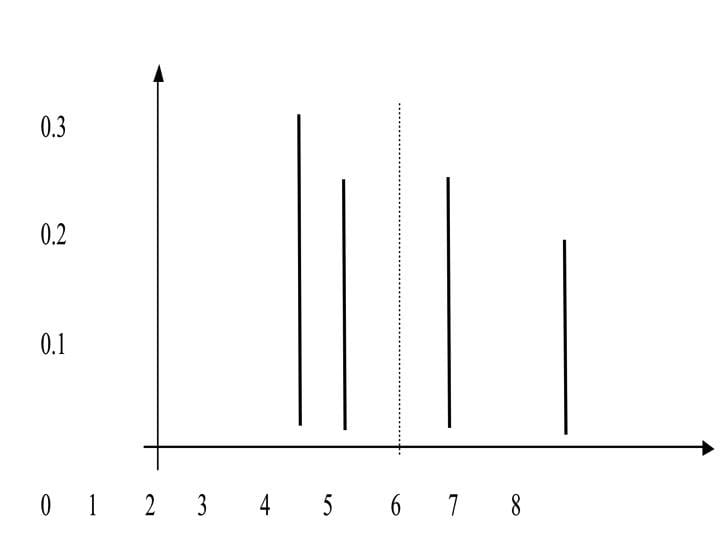
נתבונן בדיאגרמת עמודות של ההתפלגויות (התוחלת מסומנת בקו מקוטע):

התפלגות א':

התפלגות ב':

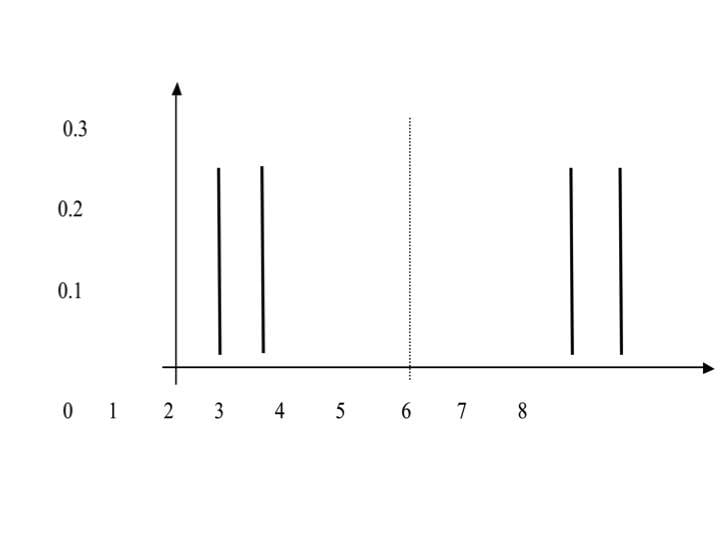
קל לראות כי התפלגות ב' מפוזרת יותר סביב התוחלת מאשר התפלגות א'. לפיכך נשתמש במדד לפיזור. מדד הפיזור הוא מספר שמאפיין למעשה את תוחלת הסטיות מהתוחלת, אך מסיבות מתמטיות החישוב שלו קצת יותר מורכב וכולל העלאה בריבוע והוצאת שורש.

מדד הפיזור הוא סטית התקן. דרך החישוב של סטית התקן במקרה של הסתברות זהה לדרך החישוב של סטית תקן של מדגם.

נוסיף טור שלישי שבו נמלא את התוחלת, וטור רביעי שבו נכתוב את הסטיה מהתוחלת (תוצאת החיסור בין הערך לבין התוחלת). בטור החמישי נעלה בריבוע את הסטיה:


הערך	ההסתברות	התוחלת	הסטיה מהתוחלת	הסטיה בריבוע
2	0.30	4	`2-4=(-2)`	`(-2)^2=4`
3	0.25	4	`3-4=(-1)`	`(-1)^2=1`
5	0.25	4	`5-4=1`	`1^2=1`
7	0.20	4	`7-4=3`	`3^2=9`
סה”כ	1.00

כעת נחשב את תוחלת הסטיה בריבוע, כלומר נכפיל את טור 2 בטור 5 ונסכם:

`3.5=9*0.2+1*0.25+1*0.25+4*0.3`

סטית התקן היא השורש של התוצאה שקיבלנו: `1.87=sqrt(3.5)`

באותו אופן נחשב את סטית התקן של התפלגות ב':


הערך	ההסתברות	התוחלת	הסטיה מהתוחלת	הסטיה בריבוע
0	0.25	4	`0-4=(-4)`	`(-4)^2=16`
1	0.25	4	`1-4=(-3)`	`(-3)^2=9`
7	0.25	4	`7-4=3`	`3^2=9`
8	0.25	4	`8-4=4`	`4^2=16`
סה”כ	1.00