דרך א' – סדרה הנדסית
נתייחס להסבר שמתייחס לגידול ההוצאה המצרפית בשלבים.
בשלב א' (שלב הפתיחה) ההוצאה המצרפית הראשונית היא E0
בשלב ב' ההוצאה המצרפית גדלה בעוד `c*E_0=c*E_0`
בשלב ג' ההוצאה המצרפית גדלה בעוד `c*[c*E_0]=c^2*E_0`
בשלב ד' ההוצאה המצרפית גדלה בעוד `c*[c^2*E_0]=c^3*E_0`
וכך בכל שלב נוסף, ההוצאה המצרפית גדלה בסכום ההוצאה המצרפית שהווספה בשלב הקודם, כפול c.
סיכום כל הסכומים בשלבים השונים יוצר סדרה שצורתה:
`E_0+c*E_0+C^2*E_0+C^3*E_0+….+c^oo*E_0`
סדרת האיברים בתוך הסוגריים מכונה סדרה הנדסית, אין סופית.
מאפייניה של סדרה הנדסית אין סופית הם:
- האיבר הראשון הוא מספר a כלשהו בחזקת 1 (a1=a) וכל איבר נוסף מבוסס על אותו a, אך החזקה עולה ב-1 בצורה הבאה: `a^1+a^2+a^3+…a^oo`
- כאשר a קטן מ-1 סכום הסדרה ההנדסית היא: `1/(1-a)` סכום הסדרה שלנו הוא: `E_0*[1/(1-c)]`
נסמל את סכום הסדרה ב- EF כלומר `E_F=E_0*[1/(1-c)]`
אם נעביר את E0 לצד שמאל, נקבל שהיחס `E_f/E_0` ` ` (שהוא המכפיל) שווה ל-`1/1-c`
דרך ב' – מפגש הפונקציות
כזכור, המשק מתמקם במקום המפגש של פונקציית קו 45° ופונקציית עקומת ההוצאות הצרפיות.
במקום המפגש מתקיים שוויון בתוצאות של 2 הפונקציות.
תוצאת פונקציית קו 45° היא: `EF=YF`
תוצאת פונקציית ההוצאות המצרפיות היא: `E_F=E_0+c*Y_F`
לפיכך: `Y_F=E_0+c*E_F`
כשנשנה את סדר האיברים נקבל:`Y_F/E_0=1/(1-c)`
נציב EF במקום YF, כלומר ( YF= EF) ונקבל: `E_F/E_0=1/(1-c)`,
`E_F/E_0` הוא המכפיל, שווה ל- `1/(1-c)`
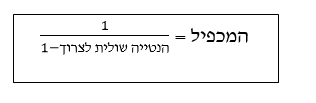
`E_F/E_0` הוא המכפיל, שווה ל- `1/(1-c)`
דרך ג' – באמצעות נגזרת
הקדמה
כל שינוי ב-E0 גורם לתזוזה של נקודת המפגש בין פונקציית קו 45° לפונקציית ההוצאות המצרפיות (להלן 2 הפונקציות).
כדי לחשב את השפעת השינוי ב-E0 על Y, עלינו להציג את Y כפונקציה של E0.
את Y כפונקציה של E0 קל לבנות לאור השיוויון שקיים בתוצאות 2 הפונקציות בנקודת המפגש שלהן.
צורת פונקציית קו 45° היא: `E=Y`
צורת פונקציית ההוצאות המצרפיות היא: `E=E_0+c*Y`
בנקודת המפגש מתקיים השיוויון: `Y=E0+c*Y`
כאשר נשנה את סדר האיברים נקבל: `Y=E_0/(1-c)`
אם נהפוך את E0 מנתון קבוע למשתנה נקבל את Y כפונקציה של E0. תוצאת הנגזרת של הפונקציה היא: `f'(y)=1/(1-c)`
הנגזרת מציינת את מספר היחידות המתווספות ל- Y בגין כל תוספת של 1 יחידה ב-E0 וזוהי בדיוק הגדרת המכפיל.
הפונקציה `Y=E_0/(1-c)`, כאשר 0.6=C מוצגת בתרשים 800.
הערה: בדר”כ כאשר הופכים נתון קבוע למשתנה מוחקים בסימול את הסימן 0 מימינו.
כלומר E0 הופך ל- E. אנו לא נוהגים כך כאן ומשאירים את ה- 0 כדי להדגיש שהמשתנה מתייחס רק להוצאה המצרפית שקיימת בתפוקה 0.
הצגה גרפית של המכפיל
נציג את המכפיל באמצעות 2 תרשימים, 900 ו- 901. בתרשים 900 מתוות 2 עקומות של הוצאות מצרפיות שבהן C = 0.6.
באחת E0=2, ובשנייה E0=3.
כאשר `E_0=2` , `Y=5` (2 * המכפיל).
המכפיל = `1/(1-0.6)`
המכפיל = `1/(1-0.6)`
כאשר `E_0=3` , `Y=7.5` (2 * המכפיל).
המכפיל = `1/(1-0.6)`
המכפיל = `1/(1-0.6)`
כל תוספת של 1 ש”ח ל-E0, מוסיפה 2.5 ש”ח ל- Y (לתמ”ג).
בתרשים 901 משורטטת הפונקציה: `Y=1/(1-c)E_0` שבה y הוא פונקציה של E0) E0 הוא משתנה).
כאשר C=0.6, כל תוספת של 1 ש”ח ב-E0 תורמת לגידול של 2.5 ש”ח ב- y.
תרשים 900
הפונקציות:
- `E=2+Cy`
- `E=3+Cy`
- `E=y`
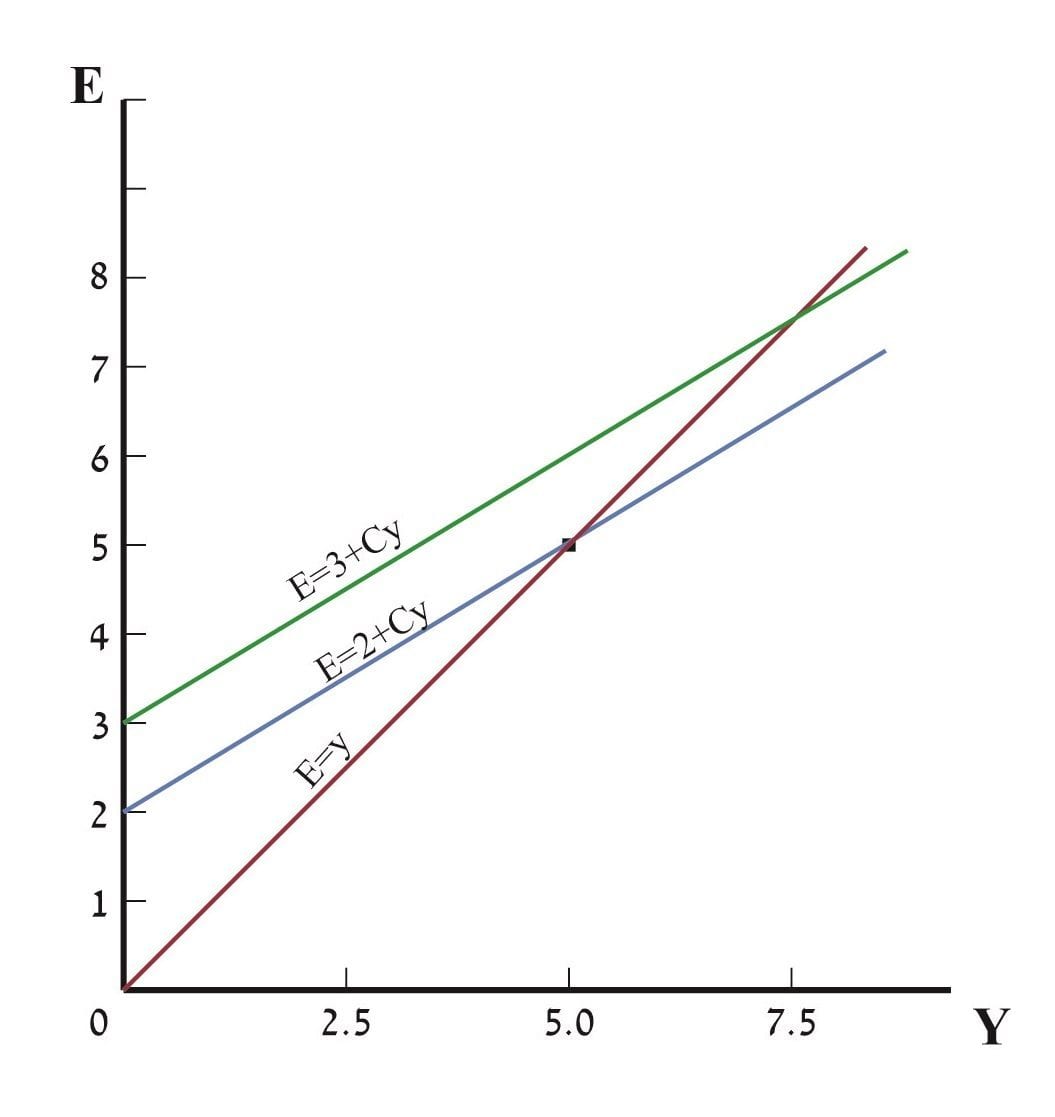
תרשים 901
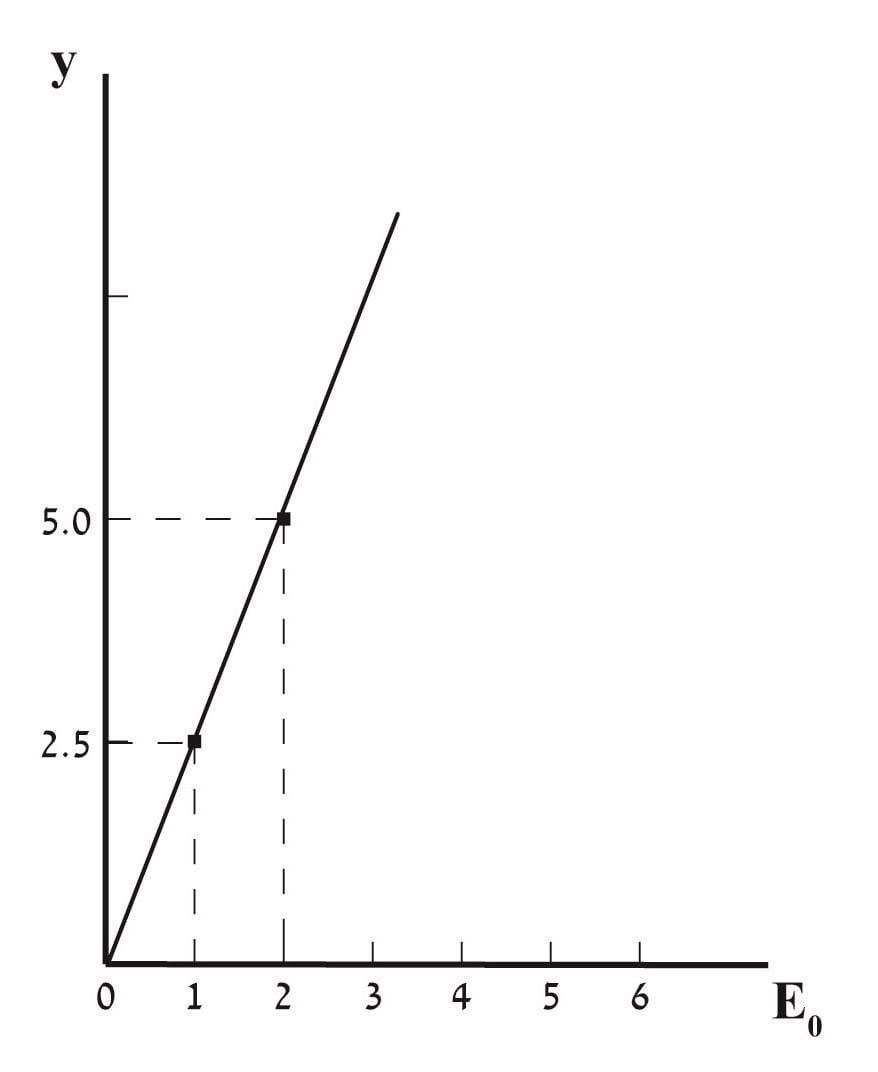
הפונקציה `Y=1/(1-c)E_0` כאשר C = 0.6
