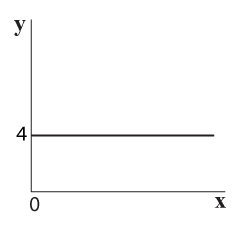דוגמה א'
f (x,y) = x·y
גזירה לפי x
הפונקציה הופכת להיות: f(x,Y) = Y·x
והנגזרת: fx(x,Y) = Y
פרשנות
כאשר, לדוגמה, Y=1, נותרת מהפונקציה רק רצועת רוחב 1.
צורתה: קו אלכסוני במישור x, z שנוסחתו: f(x) = x.
שיפועיה: 1 לכל אורכה [fx(x,Y) = 1]
כאשר Y=5, מהפונקציה נותרת רק רצועת רוחב 5.
צורתה: קו אלכסוני במישור x, z שנוסחתו f(x) = 5x.
שיפועיה: 5 לכל אורכה [fx(x,Y) = 5]
כאשר Y=0, מהפונקציה נותרת רק רצועת רוחב 0.
צורתה: קו המתלכד עם ציר x במישור x, z, שנוסחתו f(x) = 0
שיפוע: השיפוע הוא 0 לכל אורך הקו.
גזירה לפי y
הפונקציה הופכת להיות: f(x,y) = X·y
והנגזרת: fy(x,y) = X
פרשנות
בדומה לפרשנות המתייחסת לגזירה לפי x.
הצגה גרפית
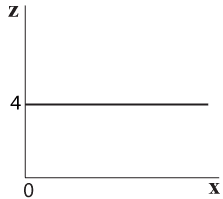
תרשים 5.23 מציג את צורת הפונקציהf(x,Y) = Y·x, כאשר y=4.
ההצגה מתבצעת משתי נקודות מבט, מלמעלה ומלפנים (מציר ה x).
כאשר אנו מתייחסים רק לרצועת רוחב 4, משתנה גם צורת הפונקציה וסימולה ל:f(x)=4x . מצורת הפונקציה ניתן ללמוד שהיא בצורת קו ישר ששיפועו 4.
תרשים 5.23
מבט למעלה מבט מלפנים
הרצועה מתלכדת עם קו הרוחב 4
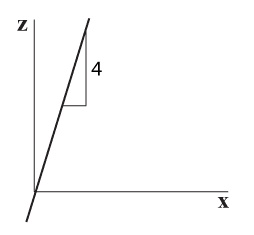
תרשים 5.24 מציג את הנגזרת של רצועת רוחב 4 במבט מלפנים (הצירים הם x ו- z). השיפוע הוא 4 בכל ערך של x (לכל אורך הרצועה).
תרשים 5.24