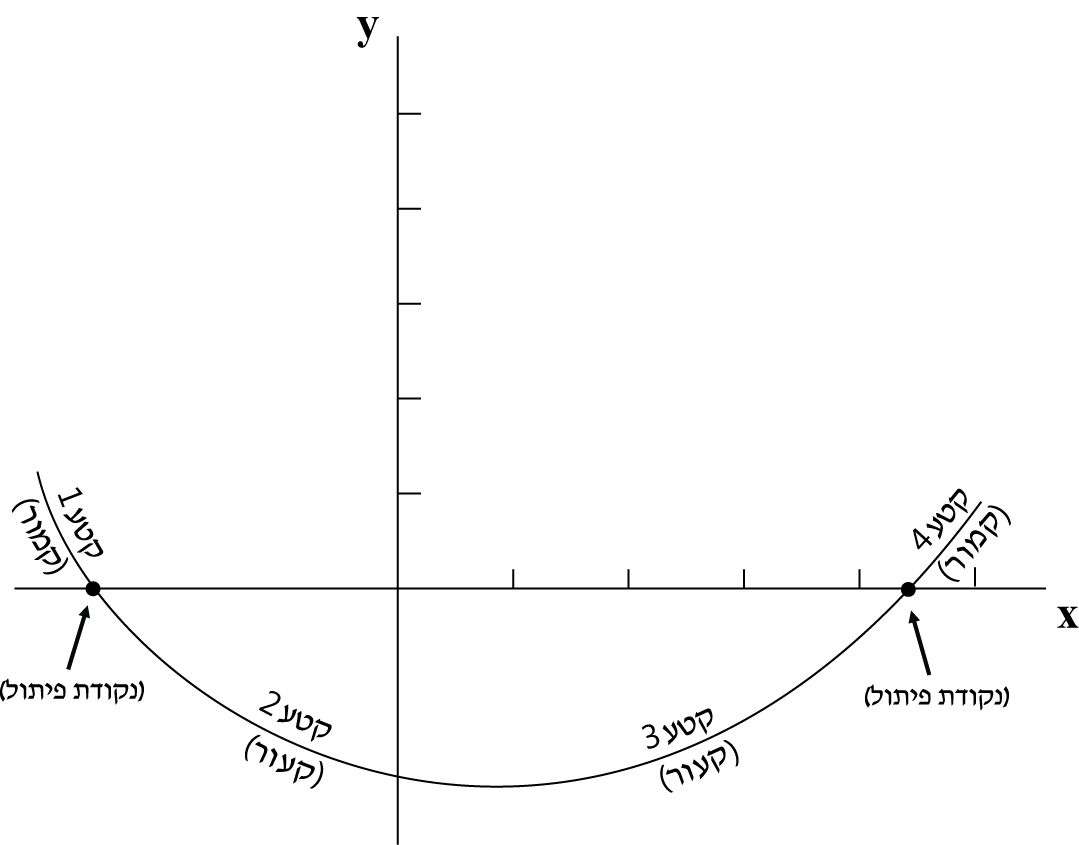
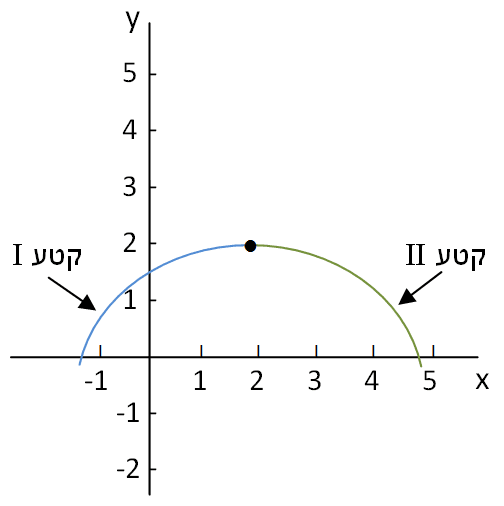תת-פרק זה נועד לחדד את ההסברים בתת-הפרק שקדם לו.
תרשים 3.5 – תוואי הפונקציה תרשים 3.6 – תוואי הנגזרת הראשונה
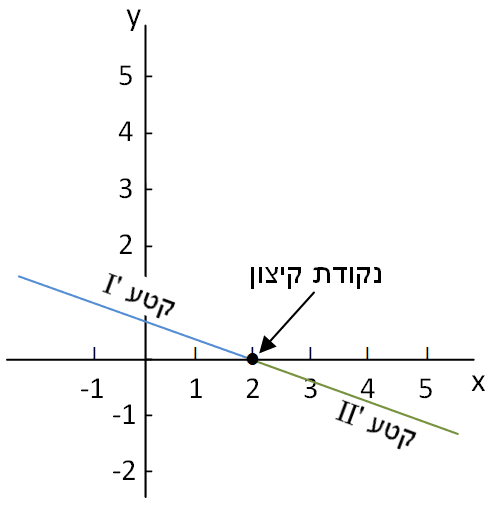
(קטע II בתרשים 3.5 וקטע II' בתרשים 3.6).
כשהפונקציה בשיפוע 0 הנגזרת חותכת את ציר ה- x
השלכות מתוצאות הנגזרת על תוואי הפונקציה
- כשהנגזרת חיובית אנו יודעים שהפונקציה עולה, אך לא מעבר לכך. אנו לא יודעים את צורתה המדוייקת. היא יכולה להיות קעורה, קמורה או לינארית.
- כשהנגזרת שלילית אנו יודעים שהפונקציה יורדת, אך לא מעבר לכך. אנו לא יודעים את צורתה המדוייקת.
- כשהנגזרת שווה ל-0 אנו יודעים שהפונקציה עשויה להיות בנקודת קיצון. כדי לוודא אם זו נקודת מקסימום או מינימום עלינו למצוא את תוואי הנגזרת משני צידיה.
ההשלכות של תזוזת הפונקציה במישור הצירים, על תוואי הנגזרת
(תרשימים 3.7, 3.8, 3.9 ו-3.10)
תזוזה אנכית של הפונקציה (תרשימים 3.7 ו- 3.8)
תרשימים 3.7 ו- 3.8 מבוססים על תרשימים 3.5 ו- 3.6.
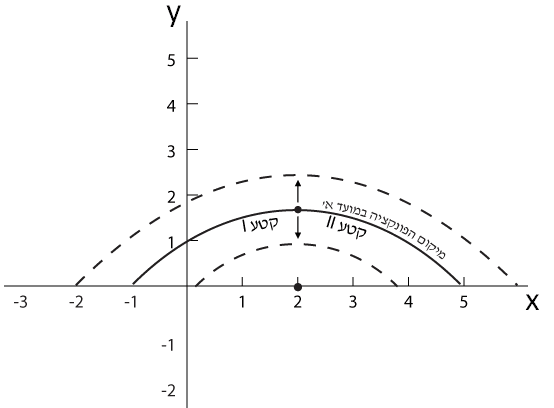
תזוזה אנכית של הפונקציה ממיקומה במועד א', הן כלפי מעלה והן כלפי מטה, כפי שמוצג בתרשים 3.7, לא משנה את התוואי הסכמטי של הנגזרת (הקווים המקווקוים בתרשים 3.7 מייצגים את מיקום תוואי הפונקציה בתזוזות האנכיות).
תרשים 3.7 – תזוזה אנכית של הפונקציה
תרשים 3.8 – תוואי הנגזרת
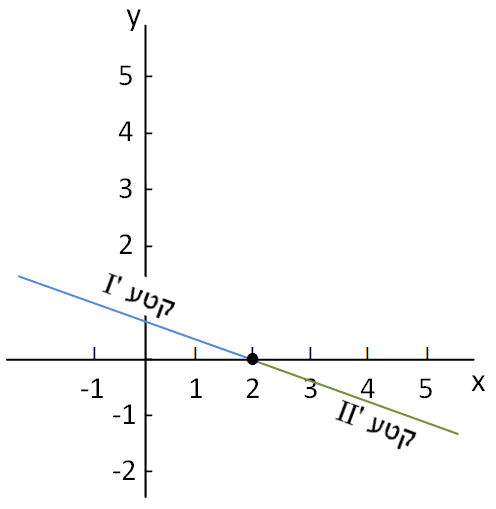
תזוזה אופקית של הפונקציה (תרשימים 3.9 ו- 3.10)
תרשימים 3.9 ו- 3.10 מבוססים על תרשימים 3.7 ו- 3.8.
תזוזה אופקית של הפונקציה, ימינה או שמאלה, גורמת במקביל לתזוזה באותו כיוון של התוואי הסכמטי של הנגזרת.
תרשים 3.9 – תזוזה אופקית של הפונקציה 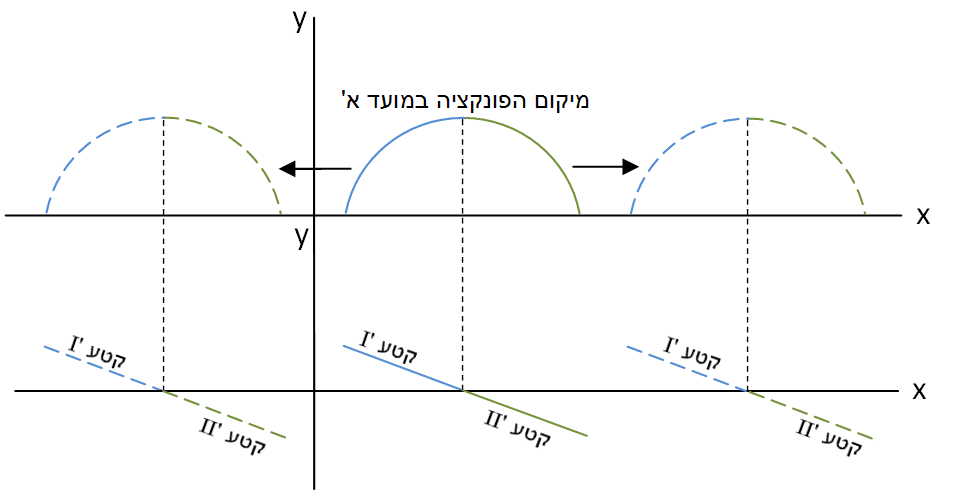
תרשים 3.10 – תזוזת הנגזרת
הקשר בין תוואי הפונקציה לתוואי הנגזרת השנייה
תרשים 3.11 – תוואי הפונקציה תרשים 3.12 – תוואי סכמטי של הנגזרת השנייה
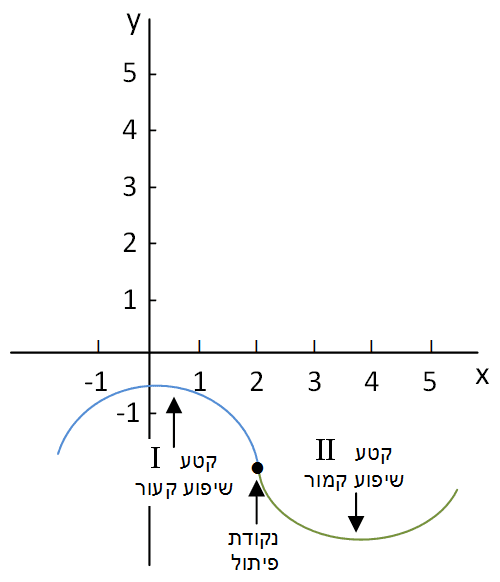
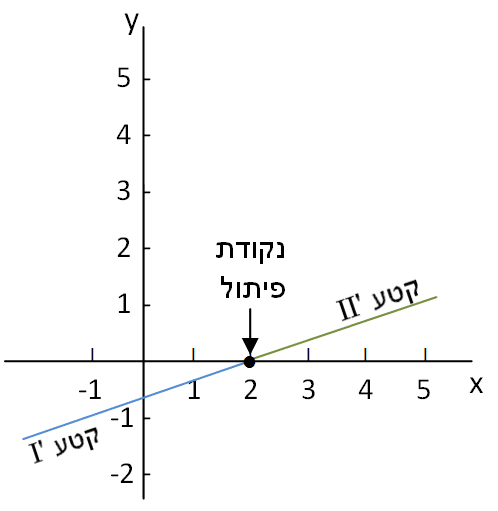
תרשים 3.13 – תוואי הנגזרת השנייה