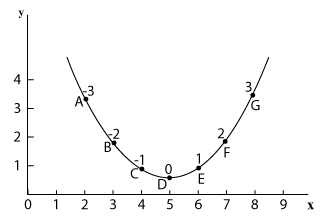
בתרשים 3.2 מוצגת הפונקציה:` f(x)=1/2x^2-5x+c`
(ה-c תלוי בנקודת חיתוך עם y)  ומתחתיה הנגזרת שלה: `f'(x)=x-5`

בתרשים 3.3 (בהמשך) מוצגת הפונקציה: ` f(x)=1/2x^2-5x+c`

(ה-c תלוי בנקודת חיתוך עם y) ומתחתיה פונקציית הנגזרת שלה: `f'(x)=-x+5` .

ב- 2 התרשימים, ציר ה- x של פונקציית הנגזרת זהה לזה של הפונקציה המקורית.

המספרים לצד הנקודות בפונקציה המקורית, מציינים את שיפוע הפונקציה באותן נקודות, כפי שהתקבלו מתוך הנגזרת שמתחתיה. שכן, תוצאת הנגזרת בערך-x כלשהו נוקב בשיפוע הפונקציה באותו ערך של x.

תרשים 3.2

 המחשת המשמעות של הנגזרת ב'

 

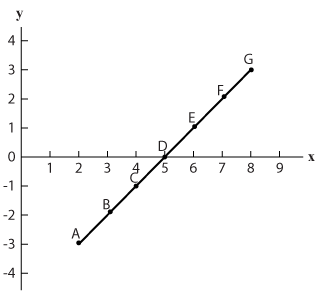
לדוגמה, בתרשים 3.3:

  1. כאשר x=3, תוצאת הנגזרת היא 2 (בנקודה B בנגזרת, `f'(-3)=-3+5`) וזה השיפוע של הפונקציה המקורית באותו ערך (נקודה B בפונקציה).
  2. כאשר x=5, תוצאת הנגזרת היא 0 (נקודה D בנגזרת) וזה השיפוע של הפונקציה המקורית באותו ערך (נקודה D בפונקציה).
  3. כאשר x=7, תוצאת הנגזרת היא 2- (נקודה F בנגזרת) וזה השיפוע של הפונקציה המקורית באותו ערך (נקודה F בפונקציה).

תרשים 3.3

 תרשים 33 א

תרשים 33 ב'

 

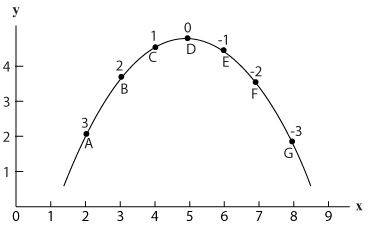
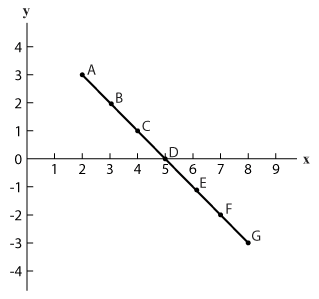
נגזרת עולה ונגזרת יורדת

הנגזרת בתרשים 3.2 עולה, והמשמעות: השיפועים של הפונקציה הולכים ועולים (עקום קמור).
הנגזרת בתרשים 3.3 יורדת. והמשמעות: השיפועים של הפונקציה הולכים ויורדים (עקום קעור).

 

שימושי הנגזרת

השימוש העיקרי בנגזרת הוא למצוא את הנקודות על הפונקציה שהשיפוע בהן הוא 0.
נקודות אלו יכולות להיות משני סוגים:
  1. נקודות קיצון – נקודות קיצון מקסימלי או נקודות קיצון מינימלי.
  2. נקודות פיתול

הן בתרשים 3.2 והן בתרשים 3.3, כאשר x=5  השיפוע = 0.