(בליווי תרשים 2.1 ו-2.2)
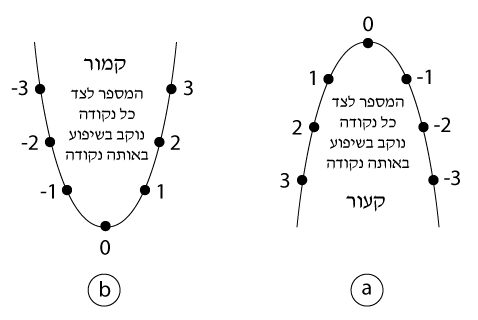
עקום קעור
כאשר מתבוננים על העקום מנקודה a שמתחתיו אנו רואים צורת קערה.
- הנקודה הגבוהה ביותר (נקודת הקיצון) היא בפסגת הקשת. קצות הקשת פונות כלפי מטה ויורדות.
- משמאל לנקודת הקיצון השיפוע חיובי (העקום עולה), אך הוא הולך וקטן. בתרשים 2.1 ככל שמתקדמים לנקודת הקיצון משמאל, השיפוע הולך וקטן מ- 3, ל- 2 ול- 1. מימין לנקודת הקיצון השיפוע שלילי (העקום יורד) והוא הולך וקטן ככל שמתקדמים.
עקום קמור
בתרשים 2.2 השיפוע משמאל לנקודת הקיצון הולך וגדל מ- (3-), ל-(2-) ול-(1-).
ככל שהמספר השלילי יותר גדול, כך השיפוע יותר קטן.
בנקודת הקיצון השיפוע 0.
כשמסתכלים על העקום שבתרשים 2.2 מנקודה b שמתחתיו, אנו רואים צורת כיפה.
המספר לצד כל נקודה, נוקב בשיפוע באותה נקודה.
תרשים 2.1 תרשים 2.2
התייחסות לשיפוע שלילי ולתלילותו
שיפוע של (2-) קטן מ- (1-), אך תלילותו יותר גדולה.
תלילות של שיפוע (3-) זהה לתלילות של שיפוע 3.
קטעי עקומים
כל קטע בפונקציה, קטן ככל שיהיה (אפילו מיקרוסקופי), משתייך לאחד מ- 3 סוגי העקומים (קו ישר, עקום קמור, עקום קעור).
פונקציות מעורבות
פונקציות המכילות יותר מסוג קטע אחד. ישנן פונקציות המכילות גם קטעים קמורים, גם קטעים קעורים וגם קטעים ישרים.
נקודת פיתול
הנקודה בפונקציה שבה קטע קעור מחליף קטע קמור וההיפך, נקראת נקודת פיתול.
איך זוכרים מה זה מה?
העקום שנראה כמו קערה הוא הקעור.
העקום שנראה כמו כיפה הוא הקמור.