כאשר ענף פועל בתנאי תחרות משוכללת, כל פירמה בענף מניחה כי היא קטנה מדי ואיננה יכולה להשפיע על המחיר בשוק, כלומר, מחיר המוצר בשוק הוא נתון לגביה.

סימולים
P – מחיר השוק
`Pi(q)`  – פונקציית הרווח.
`TR(q)` – פונקציית הפדיון.  צורת פונקציית הפדיון היא `TR(q)=P*q` .
`TC(q)` – פונקציית ההוצאות

 

פונקציית הרווח מורכבת מ- 2 פונקציות משנה:
פונקציית הפדיון פחות פונקציית ההוצאות. `Pi(q)=TR(q)-TC(q)`
מכיוון שמובן מההקשר שמדובר בפונקציות של q אפשר לוותר על רישום q לצד כל סימול.
 
הגדרות
הנגזרת של  `TC(q)`  היא:  `MC(q)` . בסימול מקוצר: `TC' = MC`
הנגזרת של  `TR(q)`   היא: `MR(q)`  . בסימול מקוצר: `TR' = MR`

תנאי הפירמה לייצור

הפירמה תרצה שיתקיימו שני תנאים:

  1. `Pi(q)` יהיה מקסימלי.
  2. `Pi(q)` לא יהיה שלילי (יכול להיות 0). כאשר תנאי 2 לא מתקיים הפירמה לא תייצר.

תנאי 1

  • הרווח המקסימלי מתקבל בכמות שבה: `Pi'(q)=0`
  • תוצאת הנגזרת היא: `Pi'(q)=P-MC(q)` .
  • והיא שווה 0 כאשר: `P=MC(q)` .

המשמעות: תנאי 1 מתקיים כאשר `P=MC(q)` .

תנאי 2

  • תנאי 2 מתקיים כאשר `[Pi_q>=0]`, כלומר `[P*q-TC(q)>=0]`.
  • אם נעביר אגפים ונחלק ב- q נקבל: `[P>=(TC(q))/(q)]`
  • נזכור שאגף ימין מייצג את ההגדרה של עלות ממוצעת `AC(q)` , ולכן תנאי 2 מקבל את הצורה הבאה: `[P>=AC(q)]` 

 

החישובים הדרושים לבחינת 2 התנאים

תנאי 1: מציאת `MC (q)`
תנאי 2: מציאת `AC (q)`

במקרה שהתנאים לא מתקיימים הפירמה לא תייצר, כלומר `0=(q)` .

 

דוגמא 1

פירמה בעלת פונקציית הוצאות: `TC(q)=q_2+3` מייצרת בתנאי תחרות משוכללת.
מחיר המוצר בשוק הוא 6 ש”ח.

כמה יחידות מהמוצר תייצר הפירמה?
מה יהיה הרווח של הפירמה?

 

פתרון

  1. נמצא את`MC(q)`  (עבור תנאי 1). התוצאה: `MC(q)=2q` .
  2. נמצא את`AC(q)`  (עבור תנאי 2). התוצאה: `AC(q)=q+3/q`  .
  3. נמצא את הכמות שבה `P=MC_q` . התוצאה: 3 יח' `(P=MC)quad=>quad2q=6`
    תנאי 1 מתקיים: הרווח המקסימלי מתקבל בייצור 3 יחידות.
  4. העלות הממוצעת עבור 3 יחידות היא 4 ש”ח `3+3/3=` , קטנה מ– 6 ש”ח (מחיר המוצר), כלומר, תנאי 2 מתקיים.

 

תוצאה: הפירמה תייצר 3 יחידות.
רווח הפירמה בייצור 3 יחידות הוא: 6 ש”ח `Pi(3)=6*3-(3^2+3)=` .

 

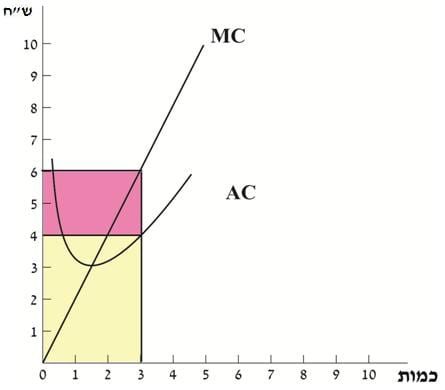
הצגה גרפית של הרווח ומרכיביו (תרשים 17)

  • שטח המלבן שקודקודיו: 3, a, 6, 0 מייצג את הפדיון.
  • שטח המלבן הצהוב מייצג את ההוצאות.
  • שטח המלבן הוורוד מייצג את הרווח.

תרשים 17

דוגמא 2

פירמה בעלת פונקציית הוצאות: `TC(q)=q^2/2+3q+5` מייצרת בתנאי תחרות משוכללת.
מחיר המוצר בשוק הוא 6 ש”ח.

כמה יחידות מהמוצר תייצר הפירמה?

 

פתרון

  1. נמצא את `MC(q)` (עבור תנאי 1). התוצאה: q+3.
  2. נמצא את `AC(q)` (עבור תנאי 2). התוצאה: `q/2+3+5/q` .
  3. נמצא את הכמות שבה `P=MC(q)` . התוצאה: q=3. הרווח המקסימלי מתקבל בייצור 3 יחידות. תנאי 1 מתקיים.
  4. `AC(3)=3/2+3+5/3=37/6=6(1)/(6` ש”ח, גדול מ- 6 ש”ח (מחיר המוצר), ולכן תנאי 2 לא מתקיים.

תוצאה: הפירמה לא תייצר (תייצר 0 יחידות).

דוגמא 3

פירמה בעלת פונקציית הוצאות: `TC(q)=5q` מייצרת בתנאי תחרות משוכללת.

מחיר המוצר בשוק הוא 6 ש”ח.
כמה יחידות מהמוצר תייצר הפירמה?

 

פתרון

  1. נמצא את `MC(q)`. התוצאה: 5 ש”ח.
  2. נמצא את `AC(q)`. התוצאה: 5 ש”ח.
  3. היות ו-MC תמיד קטן מ-P, החברה לא תפסיק לייצר. המשמעות: הרווח המקסימלי הוא באינסוף, שכן כל יחידה נוספת תורמת לרווח.
  4. AC = 5 ש”ח לכל כמות מיוצרת, קטן מ- P (6 ש”ח). תנאי 2 מתקיים תמיד.

פונקציית הרווח ממחישה את תמונת המצב. צורתה: `Pi(q)=6q-5q=q` .
הרווח שווה למספר היחידות המיוצרות. אם הפירמה תייצר יחידה אחת הרווח יהיה 1 ש”ח. אם הפירמה תייצר 1000 יחידות, הרווח יהיה 1000 ש”ח. אם הפירמה תייצר מיליון יחידות, הרווח יהיה מיליון ש”ח, וכך הלאה. כלומר, הפירמה תרצה לייצר כמה שיותר.

תוצאה: הפירמה תשאף לייצר אינסוף יחידות.

דוגמא 4

פירמה בעלת פונקציית הוצאות: `TC(q)=5q+3` מייצרת בתנאי תחרות משוכללת.

מחיר המוצר בשוק הוא 5 ש”ח.
כמה יחידות מהמוצר תייצר הפירמה?

 

פתרון

  1. נמצא את `MC(q)` . התוצאה: 5 ש”ח
  2. נמצא את `AC(q)` . התוצאה: `5+3/q` ש”ח
  3. הרווח לכל יחידה הוא 0 ולפיכך הרווח המקסימלי הוא 0 בכל רמת ייצור. כל כמות מיוצרת מקיימת את תנאי 1.
  4. `AC=5+3/q>5=P` , כלומר, לכל עלות מיוצרת העלות הממוצעת גדולה מהמחיר, ולפיכך תנאי 2 לא מתקיים.

   

תוצאה: הפירמה לא תייצר כלל.