המונופול המושלם ייצר עד לכמות שבה MC משתווה למחיר המוצר.
ההסבר: המחיר של היחידה האחרונה מהווה את הפדיון השולי של המונופול.
המחיר השולי יורד, אך לא גורם להוזלת כל היחידות שקדמו ליחידה האחרונה, כפי שקורה אצל מונופול רגיל שקובע מחיר אחיד.
דוגמא 1
| נתונים | |
| פונקציית העלות | `TC(Q) =Q^2` |
| פונקציית הביקוש | `P=90-Q` |
- איזה כמות המונופול המושלם ימכור? מהו סכום הפדיון וסכום הרווח?
- איזו עסקה יציע לצרכן, אם יחליט לפעול לפי תמחור חבילות?
- איזו עסקה יציע לצרכן, אם יחליט לפעול לפי תמחור דו-תעריפי?
| הפתרון | ||
| כמות הייצור | 30 יח׳ | `((MC),(2Q))=((P),(90-Q))` |
| התמורה | ₪2,250 (חישוב על בסיס הטרפז) | `((90+60)*30)/(2)` |
| רווח המונופול | ₪1,350 | `(2250-30^2=)` |
תמחור חבילות
30 יח' תמורת 2,250 ש”ח.
תמחור דו תעריפי
| 30 יח׳ במחיר אחיד של 60 ש״ח. סה״כ | ₪1,800 |
| +דמי כניסה | ₪450 |
| סה״כ | ₪2,250 |
עודף היצרן,עודף הצרכן והרווחה החברתית
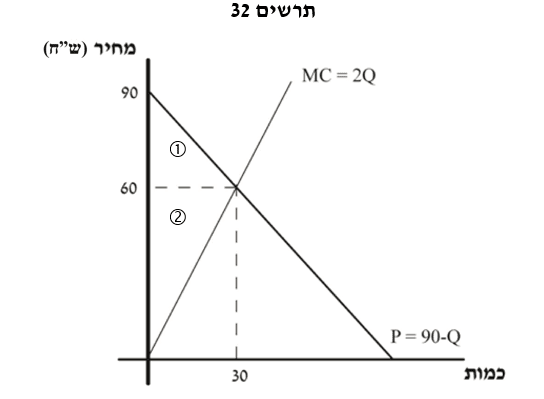
עודף היצרן הוא הפדיון של היצרן (2,250) פחות העלות המשתנה של הייצור, המיוצגת ע”י שטח המשולש שמתחת ל- `MC` (זָהֵה משולש זה בתרשים 32).
נחשב שטח זה. התוצאה: ש”ח ` (30*60)/(2) = 900`
עודף היצרן: 1,350 ש”ח `[2250-900]=`
עודף הצרכן: 0
הרווחה החברתית: 1,350 ש”ח `[1350+0]=`
התפלגות הרווחה החברתית בשוק חופשי (בליווי תרשים 32)
אילו השוק היה חופשי כמות הייצור הייתה נקבעת במקום שבו `MC` חותך את עקומת הביקוש.
| נתוני דוגמא 1 | |
| `Q` | יח׳`[2Q=90-Q]=30` |
| `P` | ₪`[P=90-Q]=60` |
| עודף הצרכן (מיוצג במשולש 1) | ₪450 |
| עודף היצרן (מיוצג במשולש 2) | ₪900 |
| סה״כ רווחה | ₪1,350 |
פרשנות
סך הרווחה החברתית בשוק חופשי שווה לרווחה החברתית במשטר של מונופול מושלם. ההבדל ביניהם הוא בחלוקה הפנימית.