חקירת תוואי הפונקציה על בסיס הנוסחה שלה בלבד
הקדמה
במסגרת חקירת תוואי הפונקציה, אנו מנסים לשרטט את התוואי, באופן סכמטי, תוך התייחסות בעיקר לנקודות הציון הבאות:
- נקודות החיתוך שלה עם ציר ה- x וה- y.
- נקודות קיצון (מינימום ומקסימום).
- תחומים בהם היא עולה או יורדת.
- נקודות פיתול.
- תחומים בהם היא קמורה, קעורה או ישרה.
טכניקת החקירה
את המידע אנו מקבלים מ- 3 מקורות:
- הפונקציה עצמה.
- הנגזרת הראשונה.
- הנגזרת השנייה.
המידע המתקבל מהפונקציה
המידע המתקבל מהנגזרת הראשונה
באמצעות הנגזרת הראשונה אנו מאתרים את הקטעים שבהם הפונקציה עולה או יורדת וכן את מיקום נקודות הקיצון, אם ישנן.
המידע המתקבל מהנגזרת השנייה
באמצעות הנגזרת השנייה אנו מוצאים את הקטעים שבהן הפונקציה קמורה או קעורה וכן את מיקומן של נקודות פיתול.
פונקציה רציפה ופונקציה מפוצלת
כאשר ניתן לשרטט את קו התוצאות של הפונקציה (= עקום הפונקציה), במשיכת קולמוס אחת (בלי להרים את היד מהדף), אזי אנו אומרים שהפונקציה רציפה.
לדוגמה, הפונקציה `f(x)=ax+b` (קו ישר) ניתנת לשרטוט במשיכה אחת.
מנגד, ישנן פונקציות שלא ניתן לשרטט במשיכה אחת.
דוגמאות
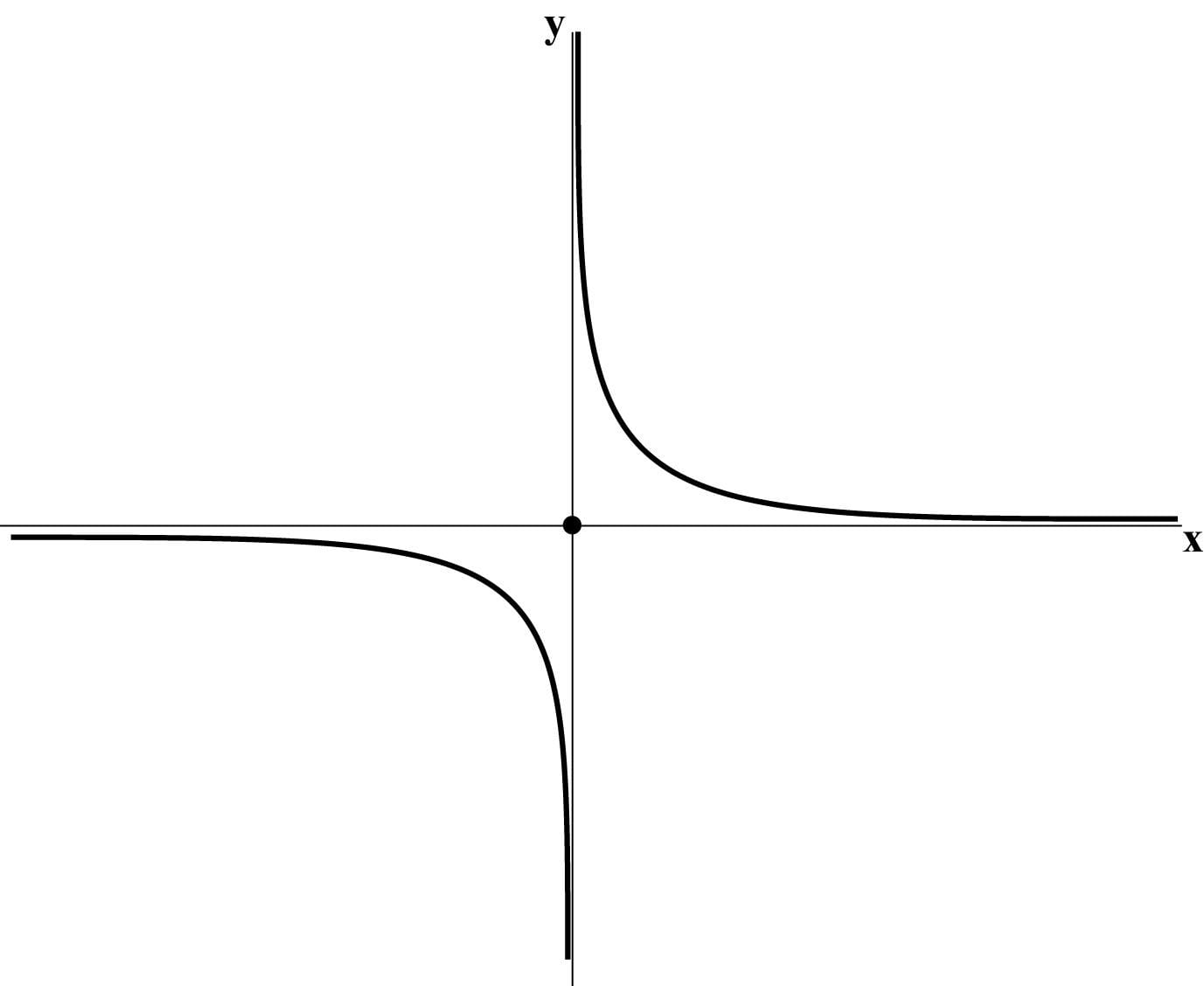
- בפונקציה `f(x)=1/x` המוצגת בתרשים הבא צריך פעם אחת להרים את היד על מנת להמשיך את השרטוט.
- הפונקציה המוצגת בתרשים הבא “קופצת” כאשר 5=x כך שצריך להרים את היד.
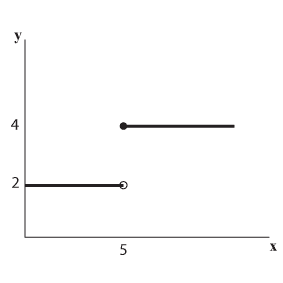
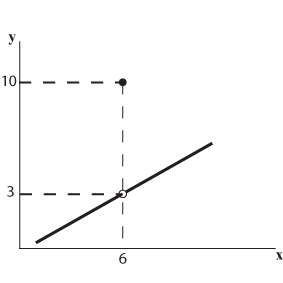
- בפונקציה המוצגת בתרשים הבא הקו הישר נקטע כאשר 6 = x ובערך זה התוצאה היא 10 (נקודה C).
מקרא
- העקום מגיע עד לערך שמתחתיו, על ציר ה- x.
- העקום לא מגיע עד לערך שמתחתיו, על ציר ה- x, אלא רק נושק לו.
המשמעות של חילוק ב- 0 (מוצג כשבר עם 0 במכנה, למשל `3/0` )
התוצאה של שבר שבו יש 0 במכנה אינה מוגדרת, אנו נוהגים לומר שהתוצאה שווה לאינסוף (∞).
כלומר: לא קיים במערכת הצירים ערך של y שמשקף את התוצאה, או במילים אחרות, לא ניתן להציב את התוצאה על מערכת הצירים.
תוצאת הפונקציה `f(x)=1/x` , בנקודה 0=x, היא `1/0` . כלומר תוצאה שאינה מוגדרת.
אין לנו עבורה נקודה במערכת הצירים. תוואי הפונקציה מוצג בתרשים שבעמוד הקודם.