1. מערכת צירים במישור x, y (תרשים 5.1)
כדי לשרטט פונקציה שטוחה, השתמשנו עד כה בצירים x ו- y שהם משטח אופקי (“רצפה”). היות וציר ה- x מייצג את המשתנה, סימול הפונקציה הוא f(x).
תרשים 5.1
2. מערכת צירים במישור x, z (תרשים 5.2)
אנו גם יכולים לשרטט פונקציה שטוחה על גבי משטח אנכי (“קיר”) שציריו x ו- z.
ציר ה- x מייצג את המשתנה וציר ה- z מייצג את התוצאות.
סימול הפונקציה: f(x) (ציר ה- x מייצג את המשתנה).
צורת הפונקציה זהה לצורה בצירים x ו- y.
תרשים 5.2
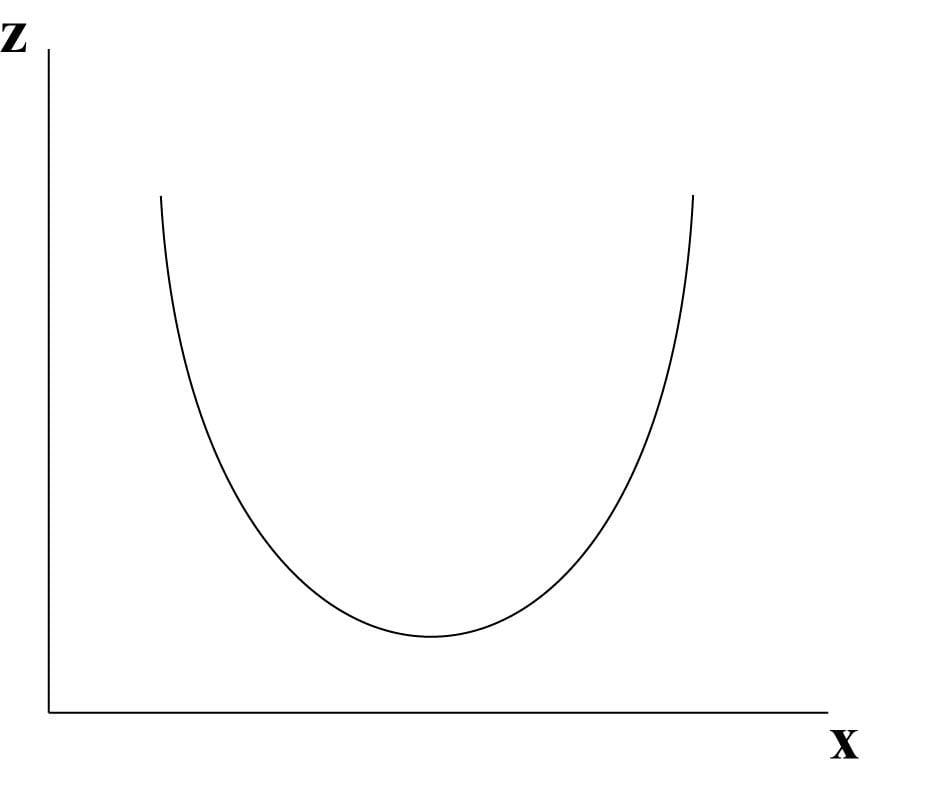
3. מערכת צירים במישור y, z (תרשים 5.3)
גם כאן המישור הוא אנכי (“קיר”).
ציר ה- y מייצג את המשתנה.
צורת הפונקציה לא תשתנה, אך סימולה כן משתנה ל- f(y).
תרשים 5.3
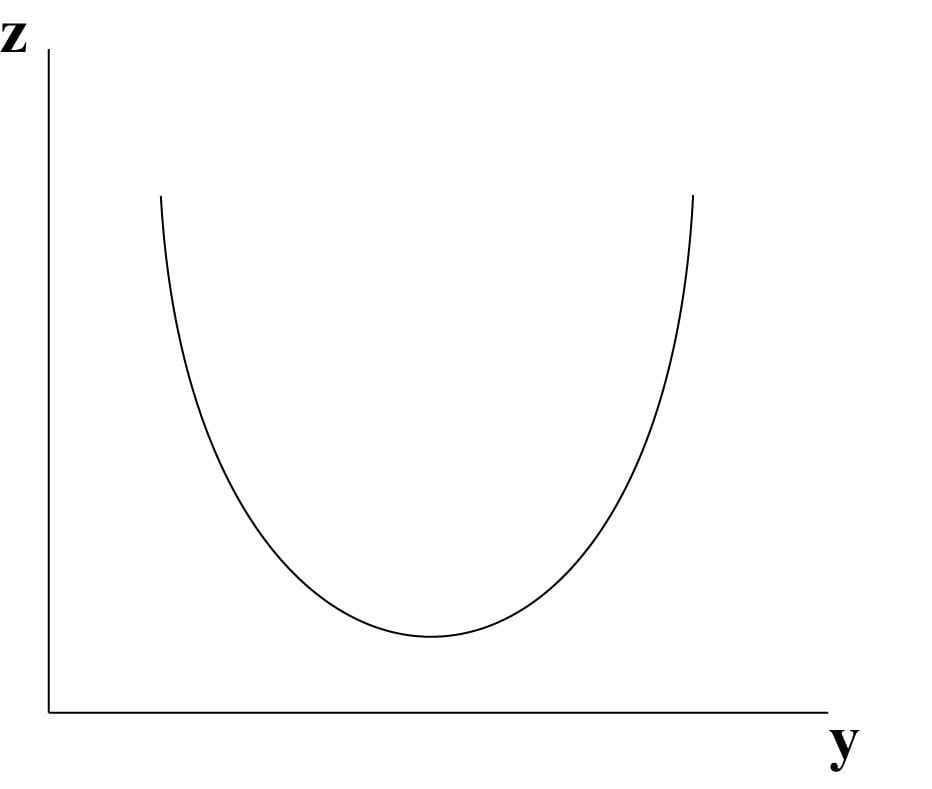
רצועה
כל תוצאות הפונקציה מעל קו כלשהו במישור הצירים, מהוות רצף של נקודות ברוחב ועובי מיקרוסקופי. רק השרטוט של תוואי הנקודות בעט או עיפרון מקנה להם קצת רוחב ועובי (העובי והרוחב שנובעים משכבת הדיו או העופרת).
לתוואי התוצאות מעל הקו במישור נקרא רצועה.
לתוצאת הפונקציה מעל קו אורך 3 נקרא רצועת אורך 3.
לתוצאת הפונקציה מעל קו רוחב 8 נקרא רצועת רוחב 8.
באופן כללי הרצועה מעל קו אורך תיקרא רצועת אורך ותתווסף לה המספור של אותו קו אורך, וכך לגבי הרצועה שמעל קו רוחב.
צורת הרצועה נגזרת ממבנה הפונקציה.
את המונח רצועה תרמנו לצורך פשטות ההסברים בהמשך. המונח לא קיים בסִפְרוּת.
תרשים 5.4
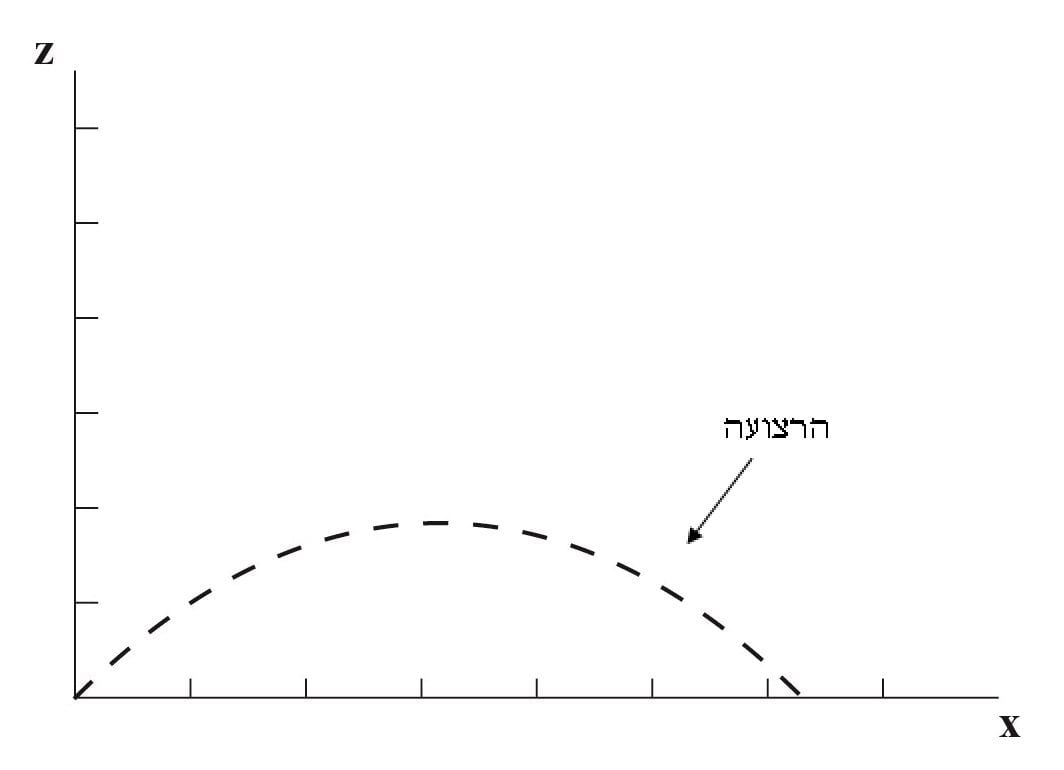
פונקציה שטוחה במרחב – המחשות
בתרשים 5.1 הרצועה מונחת בצורה אופקית במרחב ואילו בתרשימים 5.2 ו- 5.3 היא מונחת בצורה אנכית במרחב, אך למעשה אנו יכולים לשנות את מיקומה במרחב ככל שנחפוץ.
היא כמובן תמיד תישאר רצועה במרחב.
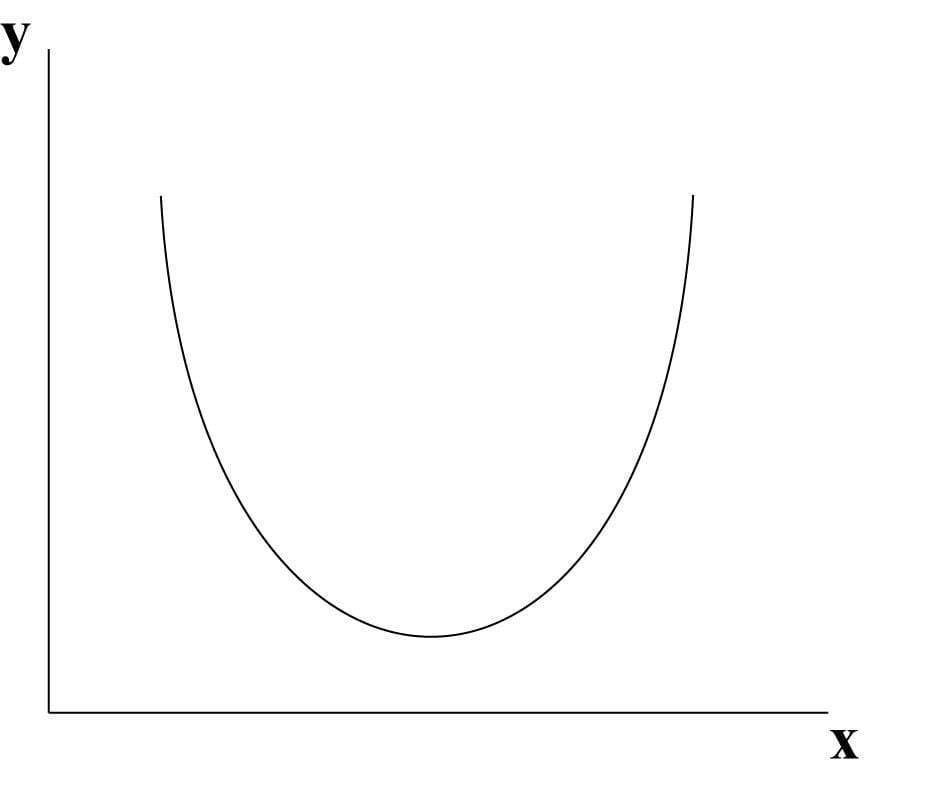


נקודות ציון הנמצאות על אותם קווי אורך או קווי רוחב
נתייחס למישור הצירים x ו- y.
מאפייני קו רוחב
בכל נקודות הציון עליו, ערך ה-y זהה (ערך ה- x משתנה).
מאפייני קו אורך
בכל נקודות הציון עליו ערך ה- x זהה (ערך ה- y משתנה).
קצת המחשות להתמצאות במרחב:
נקודות חופפות במרחב
בתרשים 5.5, הנקודה A מוצגת במישור הצירים x ו- z.
כל נקודה במרחב שנמצאת על אותו קו אורך של נקודה A (=3) ובאותו גובה (=2) היא חופפת לנקודה A עבור מי שמסתכל עליה מלפנים (מציר ה- x), באמצעות עינית בגודל של נקודה A המוצבת מולה.
במילים אחרות, מי שמתבונן על נקודה A מלפנים רואה רק את נקודה A וכל הנקודות החופפות לה מוסתרות על ידה.
תרשים 5.5
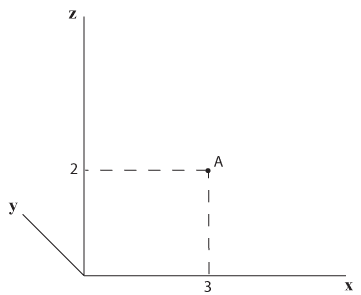
מבחינה מתמטית אפשר להתייחס לכל נקודה החופפת ל- A כאילו היא נקודה A.
כל הנקודות החופפות לנקודה A במבט מלפנים הן בעלות אותם פרמטרים של x ו- z.
רצועות רוחב חופפות במרחב
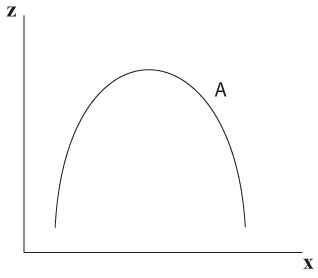
כל רצועות הרוחב במרחב, שצורתן זהה לרצועה A בתרשים 5.6 ומונחות מאחוריה, חופפות לרצועה A, למי שמסתכל מלפנים (מציר ה- x).
השיפוע בכל נקודה על רצועה A זהה לשיפוע בנקודה החופפת לו בכל הרצועות.
הפרמטרים של x ו- z זהים בכל הנקודות החופפות.
תרשים 5.6
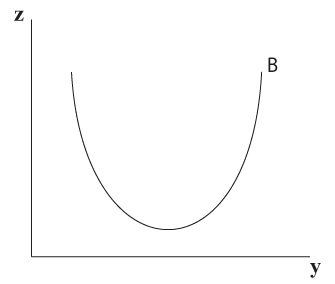
רצועות אורך חופפות במרחב
כל רצועות האורך במרחב שצורתן זהה לרצועה B בתרשים 5.7 ומונחות מאחוריה, חופפות לרצועה B למי שמסתכל מלפנים (מציר ה- y).
השיפוע בכל נקודה על רצועה B זהה לשיפוע בכל נקודה החופפת לו בכל הרצועות.
הפרמטרים של y ו- z זהים בכל הנקודות החופפות.
תרשים 5.7
עוד המחשה
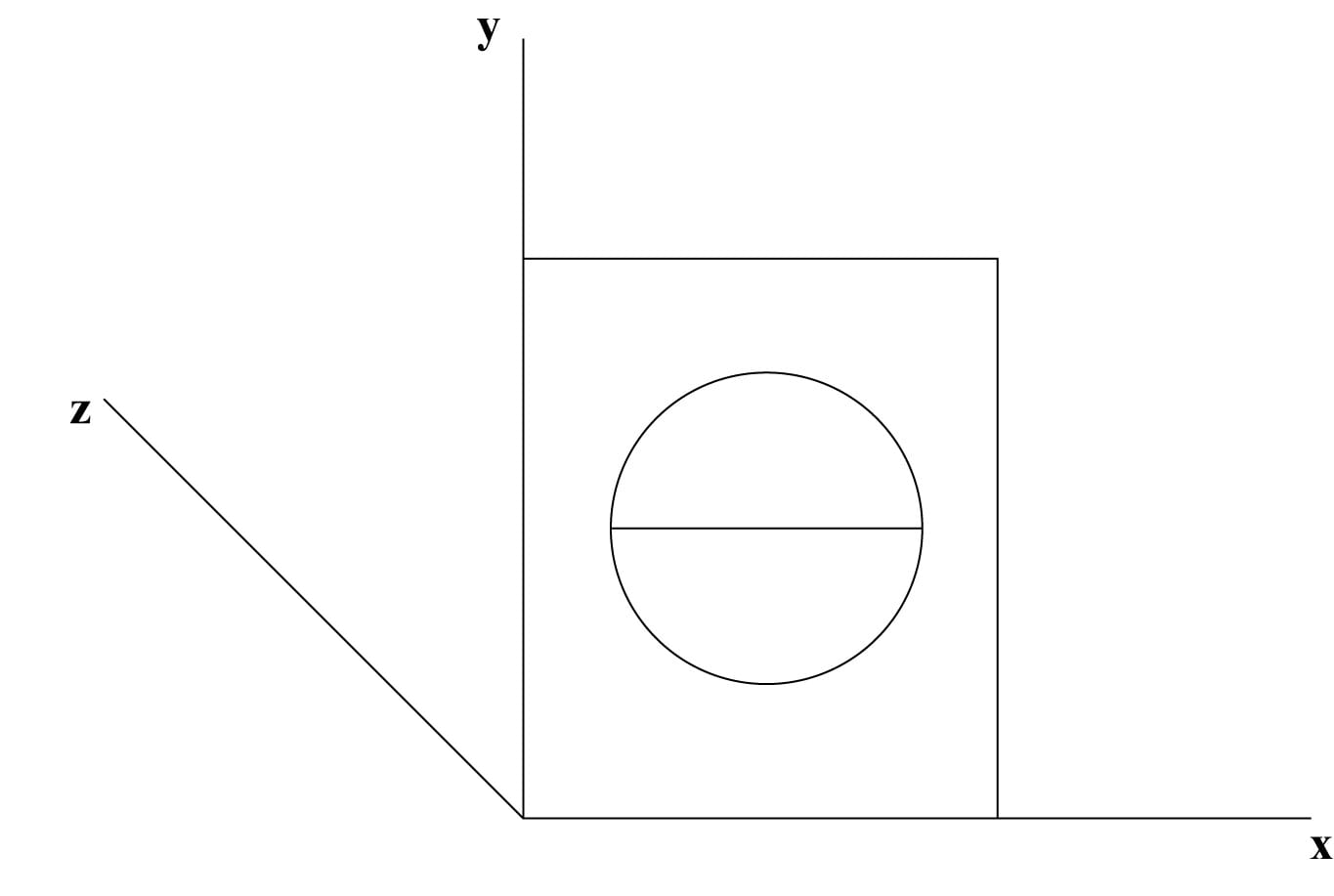
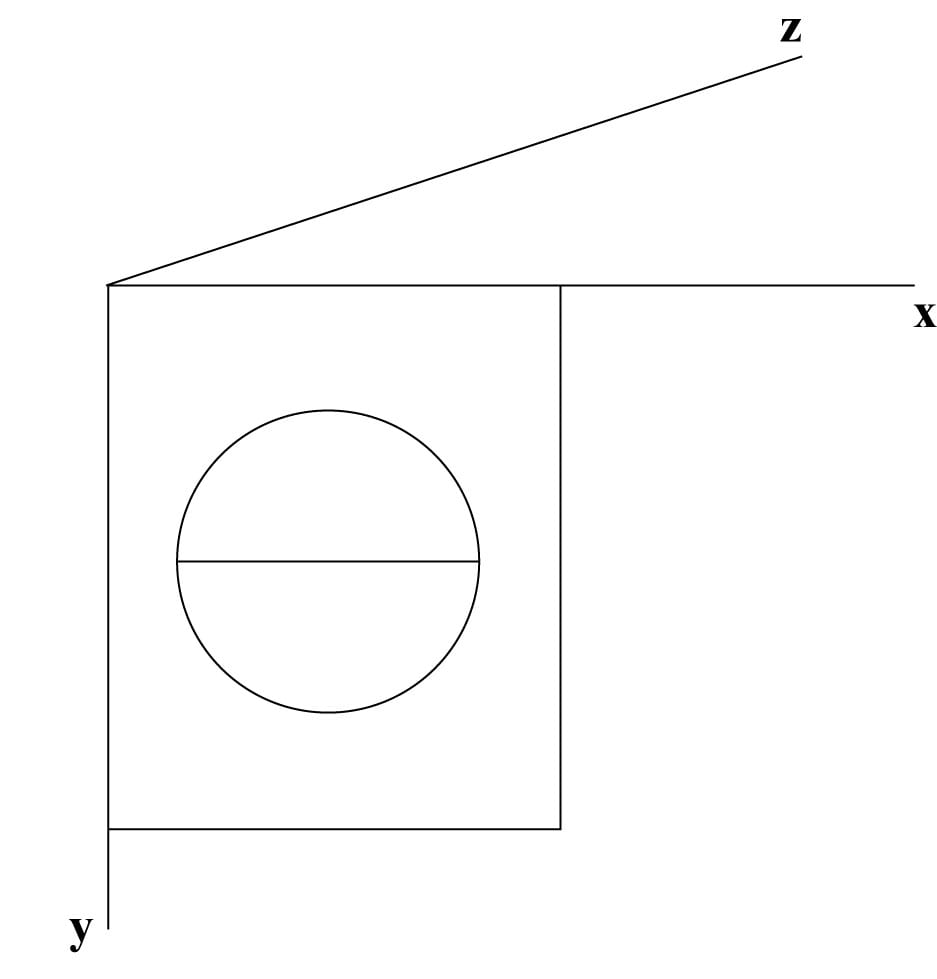
נניח שחצי כדור פלסטיק ענק מוצב על מגרש דשא מרובע כפי שמוצג בתרשים 5.8.
בפינה השמאלית של המגרש העמידו מערכת צירים של x, y ו- z.
ציר ה- x נמתח לאורך הצלע התחתונה, ציר ה- y נמתח לאורך הצלע השמאלית וציר ה- z ניצב למגרש בנקודה O.
נפרוש את חצי הכדור לרצועות רוחב מיקרוסקופיות ונותיר במגרש רק 3 רצועות שעליהן נתבונן מלפנים (ציר ה- x).
תרשים 5.8
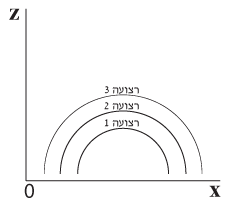
הצורות שנראה מוצגות בתרשים 5.9.
מהתרשים נראה כאילו שהרצועות ניצבות על ציר ה- x למרות שהן עמוק במגרש הדשא.
ואמנם כאשר המתמטיקאים מתבוננים ברצועות מלפנים הם מתייחסים אליהן כאילו שקירבו אותן עד לציר ה- x, שכן הרצועות המוצבות בעומק המגרש חופפות לאלו המוצבות כביכול על ציר ה- x, ומבחינת השיפועים אין הבדל בין כל הרצועות החופפות.
תרשים 5.9
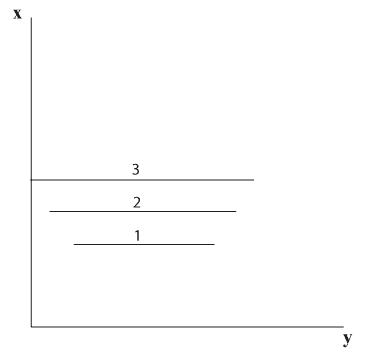
אם נתבונן ממעוף הציפור על הרצועות, נראה 3 פסים ישרים מונחים על הדשא כפי שמוצג בתרשים 5.10. אורך כל פס שווה למרחק שבין הקצוות של הרצועה.
בהתבוננות מלמעלה לא נבחין בקשתות של הרצועות.
תרשים 5.10
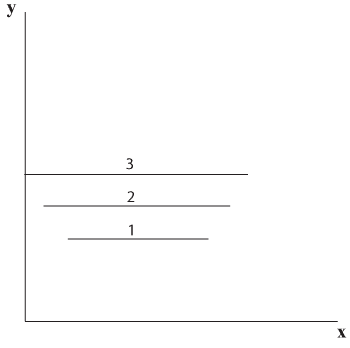
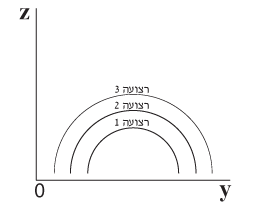
אם נציג את הצירים כמו בתרשים 5.11 ונתבונן על 3 רצועות אורך מלפנים (מציר ה- y), הצורה שנראה מוצגת בתרשים 5.12.
תרשים 5.11
גם כאן נראה שהרצועות כאילו נוצרות על ציר ה- y, למרות שהן עמוק במגרש.
תרשים 5.12
אם נתבונן ממעוף הציפור על הרצועות, נראה 3 פסים ישרים מונחים על הדשא כפי שמוצג בתרשים 5.13.
תרשים 5.13
מאותן סיבות שפירטנו קודם, כל הרצועות החופפות מייצגות אותה פונקציה של y.
דוגמה לפונקציה בת 2 משתנים בתחום הכלכלי
ירקן מוכר 2 מוצרים:
תפוזים במחיר של 10 ש”ח לק”ג.
עגבניות במחיר של 5 ש”ח לק”ג.
כמות התפוזים שנמכרת היא משתנה שנסמלו x.
כמות העגבניות שנמכרת היא משתנה שנסמלו y.
הפדיון של הירקן הוא פונקציה של x ו- y.
סימולה ומרכיביה הם: f(x,y)=10x+5y.
לכל צירוף של x ו- y מתאימה תוצאת פדיון כלשהי.





















