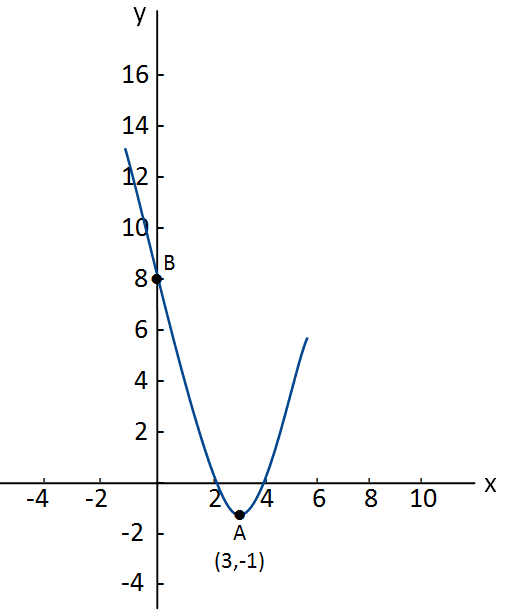- נקודת מקסימום מוחלט– הנקודה הגבוהה ביותר בכל עקום.
- נקודת מינימום מוחלט – הנקודה הנמוכה ביותר בכל עקום.
- נקודת מקסימום מקומי – נקודה ששתי הנקודות הסמוכות לה משני צידיה, נמוכות ממנה.
- נקודות מינימום מקומי – נקודה ששתי הנקודות הסמוכות לה משני צידיה, גבוהות ממנה. כמובן שכל נקודת מקסימום מוחלט היא אוטומטית נקודת מקסימום מקומי וכך לגבי נקודת מינימום.
- נקודות פיתול – (שינוי כיוון)
- נקודות החיתוך של העקום עם ציר ה-X וציר ה-Y.
- התנהגות העקום כאשר 0 =x (יורחב בהמשך).
התייחסות לנקודות פיקנטיות בפונקציה ובקטעים ממנה – חזרה והרחבה
נתייחס לכל הפונקציה ולקטעים ממנה באמצעות קו הפונקציה (=קו התוצאות) המייצג אותה. כלומר:
כל הפונקציה – מיוצגת באמצעות קו הפונקציה בכל ערכי ה- x.
מ- `x=-alpha` עד `x=alpha` `[alphaltxlt-alpha]`
לדוגמה בתחום שבין x=0 , ל- x=5. סימול: `0<=x<=5`
באופן מעשי אנו נתייחס בעיקר לקטעים ולא לכל הפונקציה.
הערות
- כמובן שכל נקודת קיצון מוחלט מהווה באופן אוטומטי גם נקודת קיצון מקומי בתת-הקטע שבו היא ממוקמת.
- כאשר מתייחסים לכל הפונקציה, לא בכל פונקציה ישנן נקודות קיצון מוחלטות (מקסימליות ו/או מינימליות).
נקודות קיצון מוחלט ומקומי – דוגמאות
- בקטע המוצג, נקודה A מהווה גם נקודת מינימום מוחלט וגם נקודת מינימום מקומי. למעשה נקודה A מהווה גם נקודת מינימום מוחלט בכל הפונקציה.
- נקודת מקסימום מוחלט בכל הפונקציה. אילו היינו משרטטים את כל הפונקציה, לא היינו מוצאים בה נקודת מקסימום מוחלט. לצד כל נקודה שנבחר ישנה נקודה גבוהה ממנה.
- נקודת מקסימום מוחלט בקטע `0<=x<=4` . אם נתייחס לקטע `0<=x<=4` , נגלה שקיימת נקודת מקסימום מוחלט שגובהה 8 (נקודה B). היא מתקבלת כאשר 0=x. בקטע זה אין נקודה גבוהה ממנה.
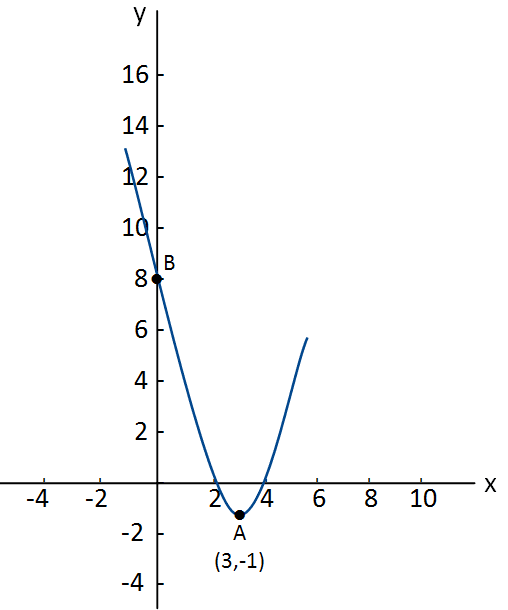
מסקנות
- ירידה ממעמד של “נקודות קיצון מוחלט” בדוגמאות שהצגנו עד כה ראינו שגם אם קיימת נקודת קיצון מוחלט בקטע מסויים, היא יכולה לרדת לדרגת “נקודת קיצון מקומי” כשמתייחסים לכל הפונקציה או לקטע יותר גדול.
- מיקום נקודות קיצון מוחלט בקטעי פונקציה הנקודות יכולות להימצא באחת מ- 2 האפשרויות הבאות:
- בקצות הקטע.
- בחפיפה עם אחת מנקודות הקיצון המקומיות בקטע.
עוד נשוב להתעמק בנקודות קיצון לאחד שנלמד מהי נגזרת וכיצד ניתן בעזרתה למצוא נקודות קיצון.