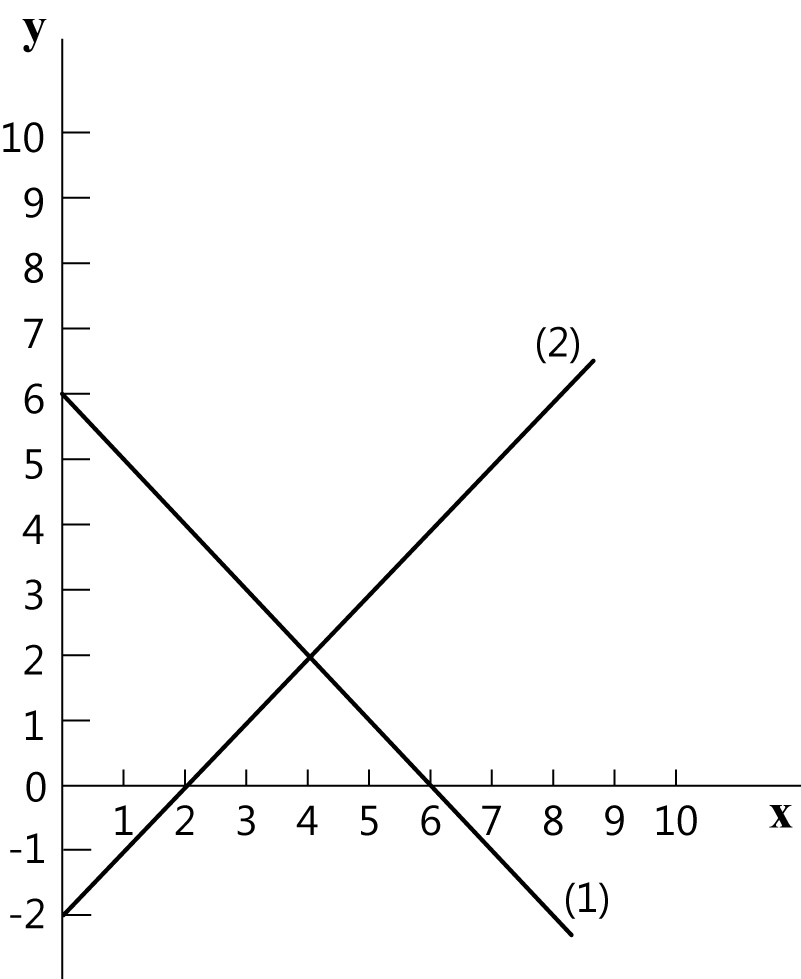חישוב נקודת החיתוך של ציר ה- x
הקו חוצה את ציר ה-x כאשר 0=y.
לדוגמה, הקו שנוסחתו `y=-3x-6`, חוצה את ציר ה-x כאשר `(-3x-6=0)` .
נפתור את המשוואה ונקבל 2-=x.
חישוב נקודת החיתוך של 2 קווים
לדוגמה, נתייחס לקו (1): `y=-x-6` ולקו (2): `y=x-2` .
בנקודת החיתוך שלהם ערך ה-x בשניהם שווה וגם ערך ה-y.
היות וערך ה- y שווה בשניהם, מתקיים השיוויון: `(x-2)=(-x+6)` .
נפתור את המשוואה ונקבל x=4.
ואז, כאשר x=4 ← y=2. כלומר נקודת החיתוך היא בנקודת הציון (4,2).
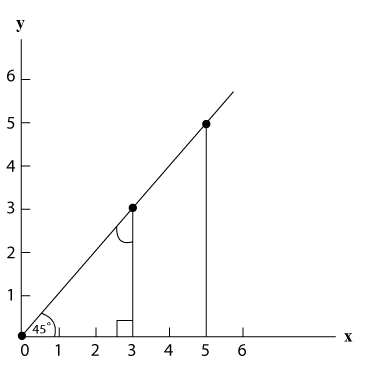
קו שיוצא מראשית הצירים ושיפועו 1
המשמעות של שיפוע 1 היא שתוספת של 1 יחידה x מוסיפה 1 יחידה y.
בתרחיש זה תמיד ערך ה-x שווה לערך ה-y והזווית בין קו הפונקציה לציר ה-x שווה ל- 450.
קו אופקי
הקו `y=0*x+b` הוא קו אופקי שכן השיפוע שלו הוא 0.
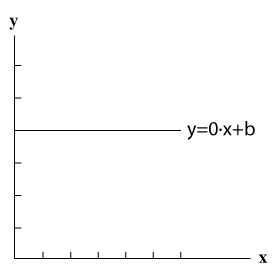
מאפייני הקו
- הוא חותך את ציר ה- y בערך b.
- הוא מקביל לציר ה- x.
המשמעות: בכל ערך של x התוצאה תהיה b.
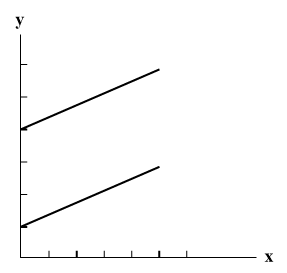
קווים מקבילים
אלו קווים בעלי אותו שיפוע (אותו פרמטר a בשניהם). קווים מקבילים אינם נפגשים לעולם.
