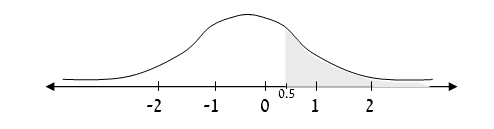
שאלה: מה ההסתברות לקבל ערכים גבוהים מ – 0.5?
תשובה: 0.3085
הסבר: את זה אי אפשר למצוא בטבלה באופן ישיר, כיוון שהטבלה נותנת את ההסתברות לקבל ערכים נמוכים יותר, ובשאלה התבקשנו למצוא את ההסתברות לקבל ערכים גבוהים יותר. את התשובה נקבל באמצעות פעולת חיסור.
סך כל השטח של ההתפלגות הוא 1, ולכן אם נפחית מ-1 את ההסתברות לקבל ערכים נמוכים מ – 0.5 (שאותה מצאנו בשאלה הקודמת), נקבל את ההסתברות לקבל ערכים גבוהים מ – 0.5: 0.3085=(0.6915-1)
למעשה התייחסנו בשאלה ל – 2 מאורעות משלימים.
- מאורע א' – ההסתברות לקבל ערך קטן מ- 0.5.
- מאורע ב' – ההסתברות לקבל ערך גדול מ- 0.5.
מאורעות עם נקודת התחלה ונקודת סוף
שאלה: מה ההסתברות לקבל ערכים בין 0 לבין 0.5? (מסומן באפור)
תשובה: 0.1915
הסבר: כדי למצוא את השטח המסומן באפור, יש לבצע את פעולת החיסור הבאה:
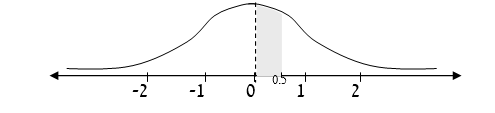
| השטח שמתחת ל 0.5 = | 0.6915 |
| השטח שמתחת ל – 0 = | 0.5000 |
| התוצאה | 0.1915 |
שאלה: מה ההסתברות לקבל ערכים בין 1.5 – לבין 1.5?
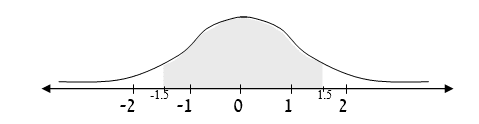
תשובה: 0.8664
הסבר: השטח שמשמאל ל 1.5 =0.9332,
השטח שמשמאל ל (1.5-)=0.0668.
החיסור שלהם ייתן את השטח המסומן בציור, שהוא ההסתברות המבוקשת.
`0.8664=(=0.9332-0.0668)`
שאלה: מה ההסתברות לקבל ערכים גבוהים מ 1.5 או נמוכים מ 1.5 – ?
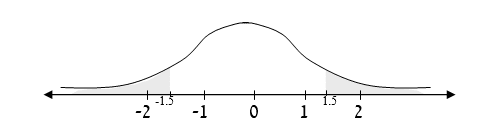
תשובה: 0.1336
הסבר:
דרך א': באופן הקל ביותר אפשר לראות שהשטח בשאלה זו הוא בדיוק המשלים ל – 1 של השטח בשאלה הקודמת.
כלומר סכום השטח בשאלה זו ושל השטח בשאלה הקודמת הוא 1. לכן אם נפחית מ – 1 את השטח שהתקבל בשאלה הקודמת, נקבל את התשובה לשאלה זו: `(1-0.8664)=0.1336`
דרך ב': נמצא בטבלה את השטח שמשמאל ל 1.5-, שהוא 0.0668. בגלל הסימטריה של הפעמון, השטח שמימין ל 1.5 הוא בדיוק אותו דבר (0.0668). לכן, סך כל השטח המסומן הוא:
