צורת רצועות הרוחב יכולה להשתנות מרצועה לרצועה וכך גם רצועות האורך.
דוגמה 1
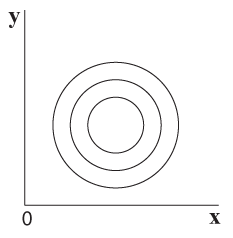
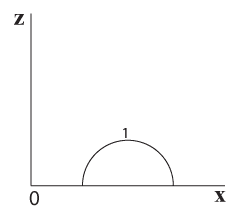
נניח שהפונקציה יוצרת מעטפת של חצי כדור עליון. רצועות הרוחב תלכנה ותגדלנה ככל שנתקדם מקצה הכדור למרכזו ותשובנה לקטון ככל שנתרחק מהמרכז, וכך גם רצועות האורך (כמו במבט מלמעלה בתרשים 5.16).
תרשים 5.15 – חצי כדור (מבט מלמעלה)
המחשת רצועות רוחב של חצי כדור
המחשת גודלן וצורתן של 7 רצועות רוחב מוצגת בתרשים 5.16.
ההמחשה נעשית באמצעות 2 נקודות מבט:
1. מבט מלמעלה
2. מבט מלפנים (מכיוון ציר x).
במבט מלמעלה הרצועות נראות כקווים ישרים המתלכדים עם קווי הרוחב (במבט מלמעלה לא רואים את צורת הקשת).
במבט מלפנים רואים בבירור את הקשתות שהולכות וגדלות.
תרשים 5.16 – מבט על רצועות הרוחב של הכדור
מבט מלמעלה מבט מלפנים (מציר ה- x)
רצועות 5-7 אינן נראות שכן הן חופפות לרצועות 1-3
המחשת רצועות אורך של חצי כדור
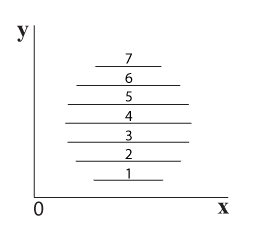
המחשת גודלן וצורתן של 7 רצועות אורך מוצגת בתרשים 5.17.
תרשים 5.17 – מבט על רצועות האורך של הכדור
מבט מלמעלה מבט מלפנים (מציר ה- y)
רצועות 5-7 אינן נראות שכן הן חופפות לרצועות 1-3
דוגמה 2
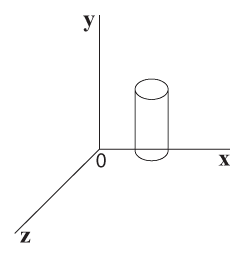
נניח שהפונקציה יוצרת מעטפת בצורת חציו העליון של צינור, שמונח במקביל לציר ה y, כפי שמוצג בתרשים 5.18.
כאן רצועות הרוחב שוות בגודלן, וכך גם רצועות האורך, כפי שנראה בתרשימים 5.19 ו- 5.20.
תרשים 5.18 – חציו העליון של גליל
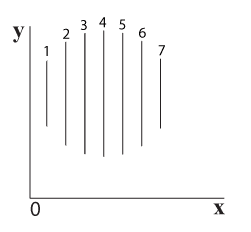
מבט על 5 רצועות רוחב מ-2 נקודות מבט מוצג בתרשים 5.19.
מבט מלמעלה מבט מלפנים (מציר x)
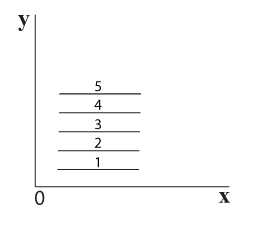
רצועות 2-5 אינן נראות שכן הן חופפות לרצועה 1
מבט על 5 רצועות אורך מ-2 נקודות מבט מוצג בתרשים 5.20.
תרשים 5.20 – מבט על רצועות האורך של הגליל
מבט מלמעלה מבט מלפנים (מציר ה- y)
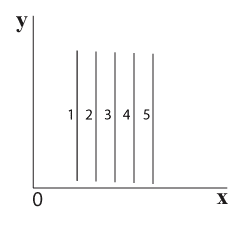
רצועות 2-5 חופפות לרצועה 1
שיפוע רצועות הרוחב מעל אותו קו אורך (למשל קו אורך 3)
במתמטיקה מקובל לנסח את המשפט בכותרת, בצורה הבאה: “שיפוע רצועות הרוחב מעל אותו ערך של x” (למשל x = 3).
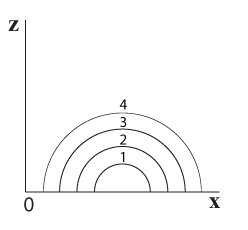
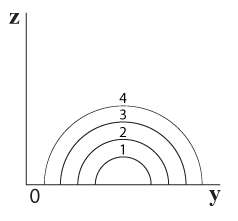
כאשר רצועות הרוחב שונות אחת מהשנייה, קרוב לוודאי שהשיפוע שלהן מעל אותו ערך של x (=קו אורך כלשהו) יהיה שונה מרצועה לרצועה, כפי שניתן לראות בתרשים 5.21 שבו מוצגות 4 רצועות רוחב של כדור.
השיפוע שלהן מעל הערך x=3 שונה מרצועה לרצועה וכך גם ביחס לכל ערך אחר של x, מלבד x=4 שבו השיפוע בכל הרצועות שווה אפס (תרשים 5.22)
תרשים 5.21 –מבט מלפנים (מציר ה x) תרשים 5.22 – מבט מלפנים (מציר ה x)
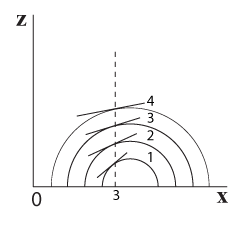
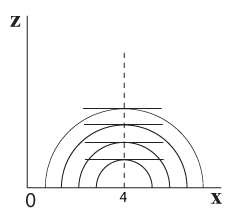
כאשר רצועות הרוחב זהות אחת לשנייה, כמו בדוגמת הגליל, השיפוע שלהן באותו ערך של x יהיה זהה, כפי שמוצג בתרשים שלהלן.
מבט מלפנים (מציר x)
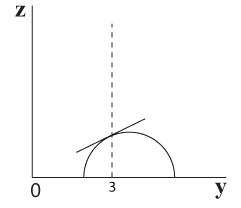
רצועות 1,3,4 מוסתרות
שיפוע רצועות האורך מעל אותו ערך של y (למשל y=4)
כאשר רצועות האורך שונות אחת מהשנייה, קרוב לוודאי שגם השיפוע שלהן מעל אותו ערך של y (=קו רוחב כלשהו) יהיה שונה מרצועה לרצועה. ואילו כאשר הרצועות זהות אחת לשנייה, גם השיפוע שלהן זהה מעל אותו ערך של y, בדיוק כפי שראינו ברצועות הרוחב.