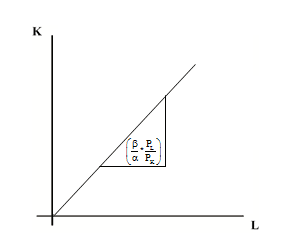
בכל אחת מפונקציות הייצור קיים יחס קבוע בין L ו- K בכל רמת תפוקה.
נמצא את היחס הזה בכל אחת מפונקציות הייצור.
`L^(alpha-1)/L^alpha=1/L quadquad(K^beta)/(K^(beta-1))=K`
1. פונקציית קוב דגלאס `X=L^alpha*K^beta`
הסל הנבחר בכל רמת תפוקה מקיים את השיוויון הבא:
| `X_L/X_K=P_L/P_K` | `X_L` – הנגזרת לפי L = `MP_L` |
| `X_P` – הנגזרת לפי K = `MP_K` |
כאשר נציב את הנגזרות ונצמצם נקבל: `(alphaL^(alpha-1)K^(beta))/(betaL^alphaK^(beta-1))=(alphaK)/(betaL)=P_L/P_K`
נבודד את K ונקבל: `K=beta/alpha*P_L/P_K*L`
פרשנות: בכל רמת תפוקה נשמר היחס הנ”ל בין L ו- K.
2. פונקציית ייצור לינארית `x=alphaL+betaK`
ישנם 3 תרחישים:
- כאשר `P_L` נחשב זול: 0=K, נשתמש רק ב- L
- כאשר`P_L` נחשב יקר: 0=L, נשתמש רק ב- K
- כאשר`P_L` גבולי: היחס בין L ל-K לא קבוע. L יכול לגדול מ- 0 ועד `x/alpha` , ו-K יקטן בהתאם.
נעלה את 2 צידי המשוואה בחזקת `1/(1-alpha)` ונבודד את K.
ריכוז התוצאות שהתקבלו בכל הפונקציות
את התוצאות שקיבלנו בכל הפונקציות ריכזנו בטבלה 1 שבה 3 טורים.
טבלה 1
|
סוג פונקציית הייצור |
התנאי לייצור יעיל |
קו ההתרחבות (היחס בין L ל- K) |
|
(1) |
(2) |
(3) |
|
קוב דאגלס `x=L^alpha*K^beta`
|
`alpha/beta*K/L=P_L/P_K` |
`K=P_L/P_K*beta/alpha*L` |
|
פונקציה לינארית `x=alphaL+betaK`
|
כאשר `P_L`זול רק L |
0 = K 0 = L |
|
פונקציה מינימום `x=min(alphaL,betaK)`
|
`alphaL=betaK` |
`K=alpha/beta*L` |
|
פונקציה אדיטיבית `x=L^alpha+K^alpha`
|
|
|
הסבר לטור 3 בטבלה 1 – קו ההתרחבות
קו ההתרחבות משקף את תוואי הסלים הנבחרים בעקבות גידול בתפוקה.
פונקציית קוב דאגלס (תרשים 7) – קו ההתרחבות בפונקציית קוב דאגלס
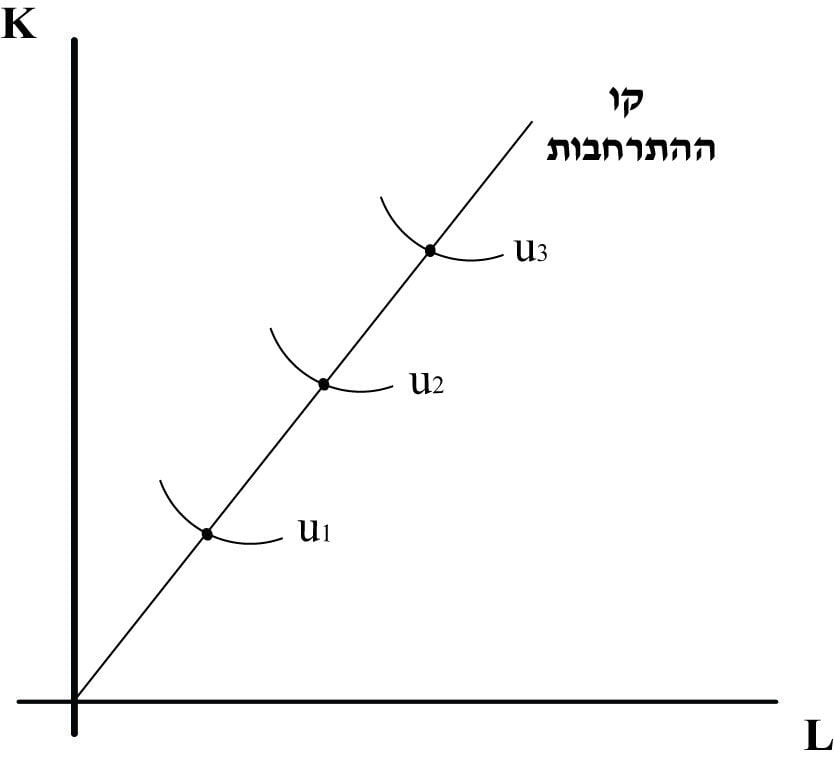
התוואי הוא קו ישר המתחיל בראשית הצירים ועולה בשיפוע של `[beta/alpha*P_L/P_K]`
פונקציה לינארית (תרשים 8) – קו ההתרחבות בפונקציה לינארית
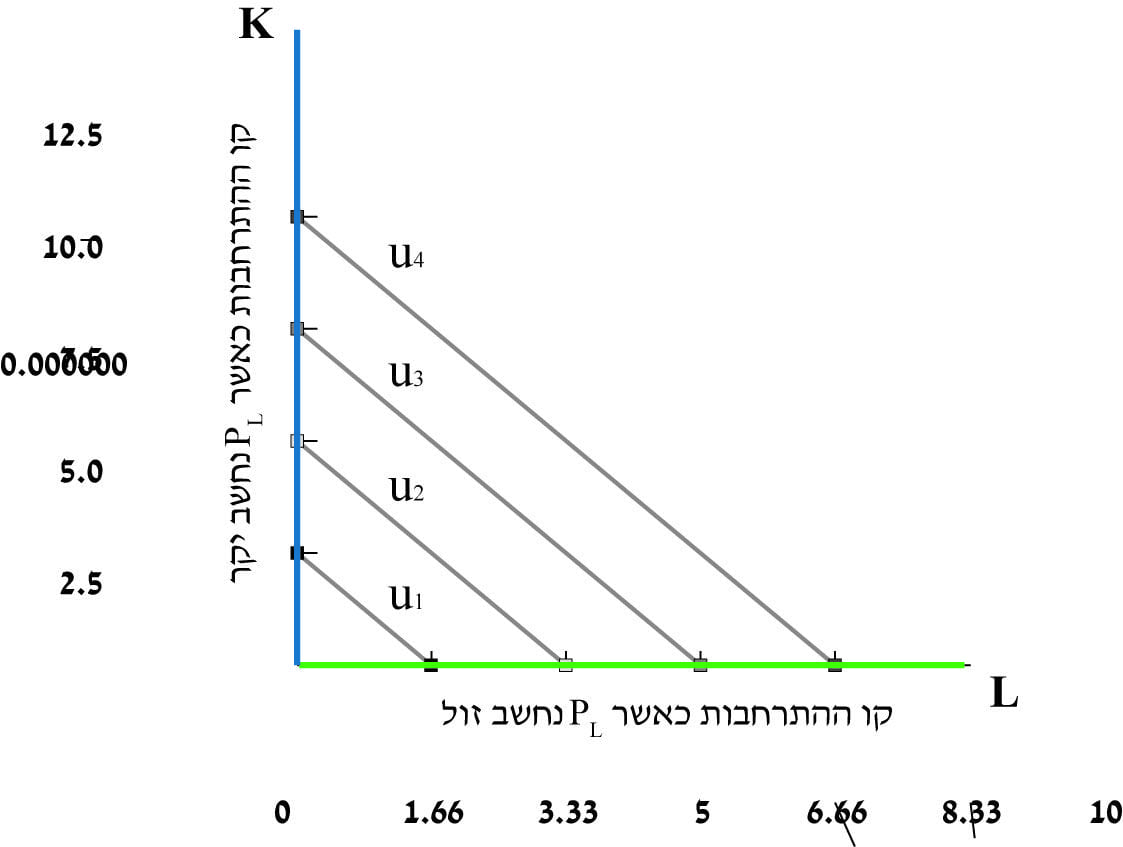
- כאשר `P_L` נחשב זול, התוואי הוא ציר ה- L.
- כאשר `P_L` נחשב יקר, התוואי הוא ציר ה- K.
פונקציית מינימום (תרשים 9) – קו ההתרחבות בפונקציית מינימום
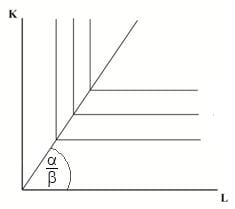
הנתיב הוא קו ישר המתחיל בראשית הצירים ועולה בשיפוע של `alpha/beta`
` `
פונקציה אדיטיבית (תרשים 10) – קו ההתרחבות בפונקציה אדיטיבית
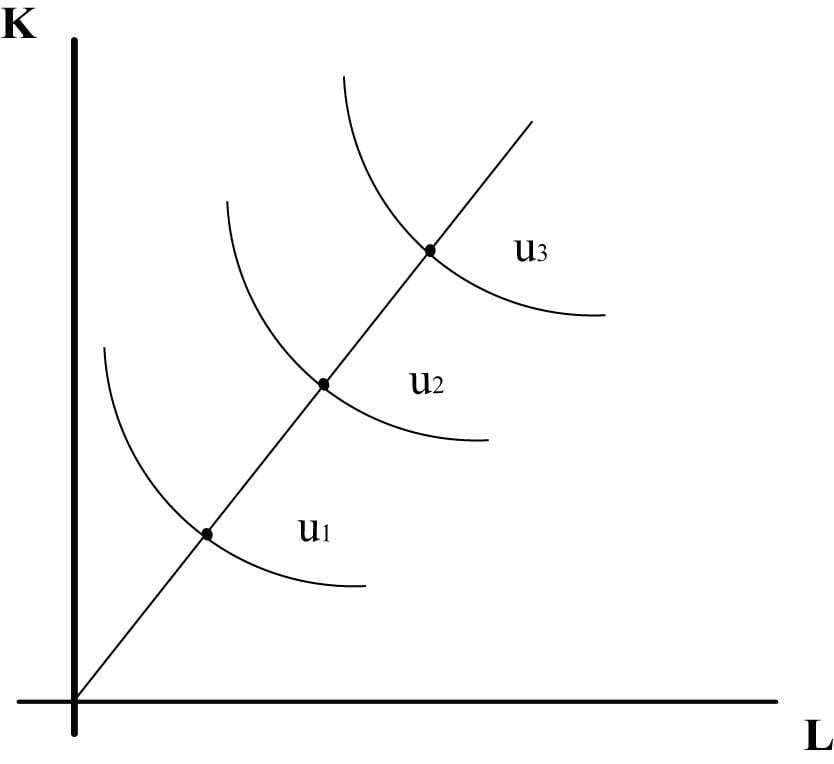
התוואי הוא קו ישר שמתחיל בראשית הצירים ועולה בשיפוע של `(P_L/P_K)^(1/(1-alpha))`
קו ההתרחבות בטווח הארוך ובטווח הקצר
תרשים 11
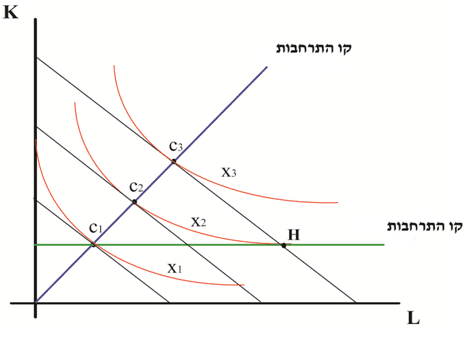
פרשנות
בטווח הקצר הייצור לא יעיל היות והתקציב הנדרש לרכישת סל H גדול מהתקציב הנדרש לרכישת סל C2 (סל H נמצא על קו תקציב שסכומו גדול מזה שעליו נמצא סל C2).
חישוב התפוקה כפונקציה של L בלבד
אם נציב בפונקציית הייצור במקום K את החלופה שלו בערכים של L כפי שמתקבל בקו ההתרחבות לטווח ארוך (טבלה 1), נקבל את x כפונקציה של L.
למשל, בפונקציית ייצור מסוג KD (קוב דאגלס) שצורתה: `x=L^alpha*K^beta`, קו ההתרחבות הוא:`K=beta/alpha*P_L/P_K*L`.
אם נציב בפונקציית הייצור את הביטוי`[beta/alpha*P_L/P_K*L]` במקום K נקבל: `x=L^alpha*(beta/alpha*P_L/P_K*L)^beta`.
x הוא פונקציה של L: `x=L^(alpha+beta)*(beta/alpha*P_L/P_K)^beta`
הצגת L כפונקציה של x
אם נבודד את L נקבל את L ע”י העלאת כל חלקי המשוואה בחזקת `1/(alpha+beta)` כפונקציה של x:
`L=1/x^(a+b)*(beta/alpha*P_K/P_L)^(beta/(alpha+beta))`
באופן דומה באפשרותנו להציג את x כפונקציה של L בכל פונקציית ייצור.
פונקציה לינארית
כאשר PL נחשב זול מתקיים K = 0 ואז `x=alphaL` .
כאשר PL נחשב יקר מתקיים L = 0 ואז לא נציג את x כפונקציה של L.
פונקציית מינימום
`x=min(alphaL,betaa/betaL)=min(alphaL,alphaL)` ולכן נקבל `x=alphaL`
גם בפונקציות הייצור האלה נוכל לבודד את L ולקבל את L כפונקציה של x.
פונקציה לינארית
כאשר `P_L` נחשב זול נקבל `L=x/alpha`
פונקציית מינימום
גם כאן נקבל `L=x/alpha`
חישוב התפוקה כפונקציה של K בלבד
באותה טכניקה שבה הצגנו את L כפונקציה של x, ניתן להציג את K כפונקציה של x.
מתחילים בקו ההתרחבות ומציגים את L כפונקציה של K, ובפונקציית הייצור מציבים במקום L את החלופה שלו בערכים של K.
לדוגמא, נתייחס לפונקציית ייצור מסוג KD.
קו ההתרחבות הוא: `K=beta/alpha*P_L/P_K*L`
נבודד את L ונקבל: `L=alpha/beta*P_K/P_L*K` (L הוא פונקציה של K).
נציב בפונקציית הייצור את הביטוי `[alpha/beta*P_K/P_L*K]` במקום L ונקבל: `X=(alpha/beta*P_K/P_L*K)^alpha*K^beta`
קיבלנו את x כפונקציה של K: `X=K^(alpha+beta)*(alpha/beta*P_K/P_L*)^alpha`
הצגת K כפונקציה של x
נבודד את K ונקבל את K ע”י העלאת כל חלקי המשוואה בחזקת `1/(alpha+beta)` כפונקציה של X:
`K=x^(1/(alpha+beta))*(beta/alpha*P_L/P_K)^(alpha/(alpha+beta))`בפרק הבא נשתמש בהצגת K ו- L כפונקציה של X.