הרווחה החברתית במצב של מונופול קטנה יותר מהרווחה החברתית במצב של תחרות משוכללת. הרווחה החברתית של תחרות משוכללת היא הרווחה החברתית המקסימלית האפשרית. בפרק זה נלמד מה יכולה לעשות ממשלה כדי להביא את הרווחה החברתית למקסימום גם כאשר במשק יש מונופול.
לממשלה יש שתי דרכים להתערבות:
- פיקוח על מחירים: קביעת מחיר מקסימום.
- שימוש במסים וסובסידיות: מתן סובסידיה ליחידה מיוצרת עם או בלי הטלת מס גלובלי על המונופול.
קביעת מחיר מקסימום
הממשלה קובעת מחיר מקסימלי למוצר, כך שלמונופול אסור לדרוש מחיר גבוה יותר מהמחיר המקסימלי.
נבחן ארבעה תרחישים לגבי מחיר המקסימום:
- `P_(MAX)>=P_m` מחיר המקסימום שקובעת הממשלה איננו אפקטיבי, כיוון שהוא לא מגביל את המונופול מלקבוע את המחיר שבו הוא מעוניין. המחיר שישרור בענף יהיה P m.
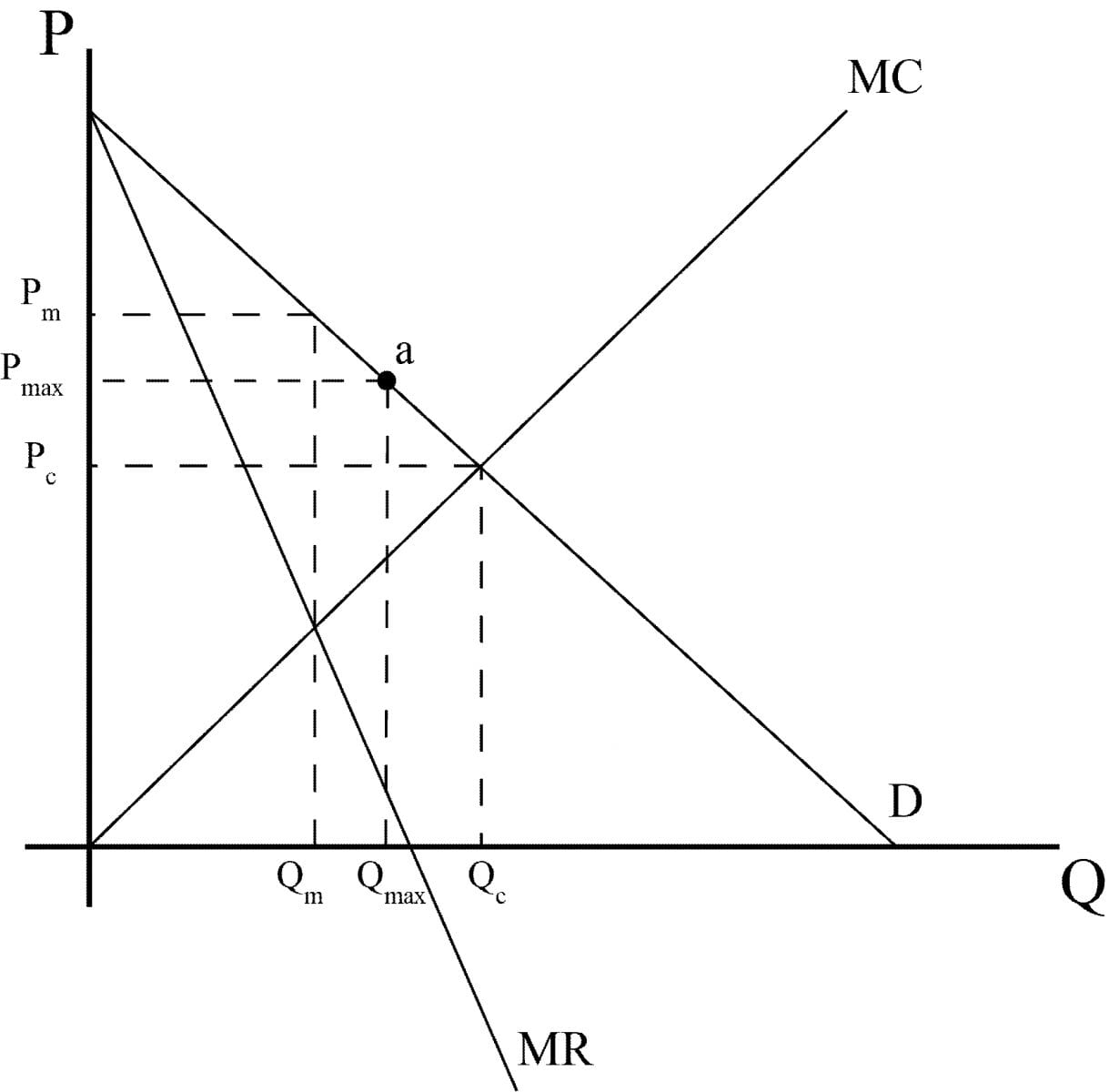
- `P_c<P_(MAX)<P_m` המונופול לא יוכל לקבוע את המחיר שהיה רוצה. במקרה זה הוא יקבע את המחיר המקסימלי המותר, P MAX. הכמות שתיוצר תהיה יותר גדולה מ- Qm, אך קטנה מ- Pm, אך הכל בתנאי שהמונופול לא מפסיד. תרשים 22 מציג את תמונת המצב בתרחיש זה. הכמות שהמונופול ייצר היא זו המתייחסת לנקודה a.
תרשים 22
- `P(MAX)=Pc` בתרחיש זה תמונת המצב זהה לזו המתקבלת בשוק חופשי, לרבות הרווחה החברתית. כל זאת רק אם רווח המונופול אינו שלילי.
- `P(MAX)ltPc` (בליווי תרשים 23) בתרחיש זה המונופול ייצר כל עוד MC לא עולה על PMAX (נקודה b) ובתנאי שהוא לא מפסיד.
הכמות שהמונופול ייצר היא Qm (קטנה מ-Qc ) במחיר Pm. הכמות המבוקשת בשוק היא QMAX, כך שיווצר בשוק עודף ביקוש שמתבטא בפער שבין QMAX ל-Qm . תרשים 23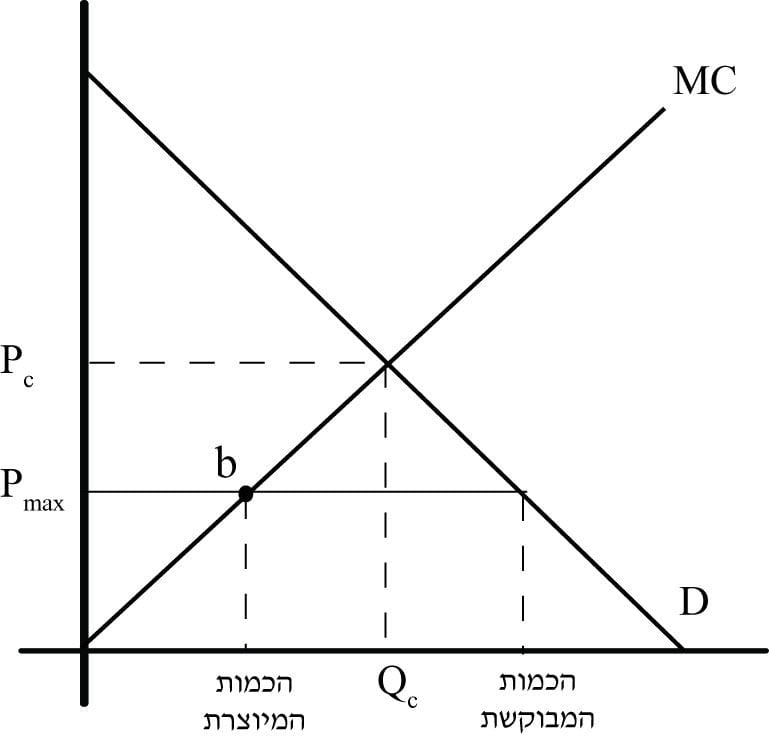
דוגמאות מספריות
דוגמא 1
|
נתוני הדוגמא: |
|
|
פונקצית העלות של המונופול: |
`TC = Q2+100` |
|
פונקצית הביקוש בשוק: |
`P = 120-Q` |
|
המחיר המקסימלי: |
`P_(MAX) =85` ש”ח |
|
פונקציית הפידיון: |
`TR=(120-Q)*Q = 120Q-Q^2` |
פתרון (בליווי תרשים 24)
תרשים 24
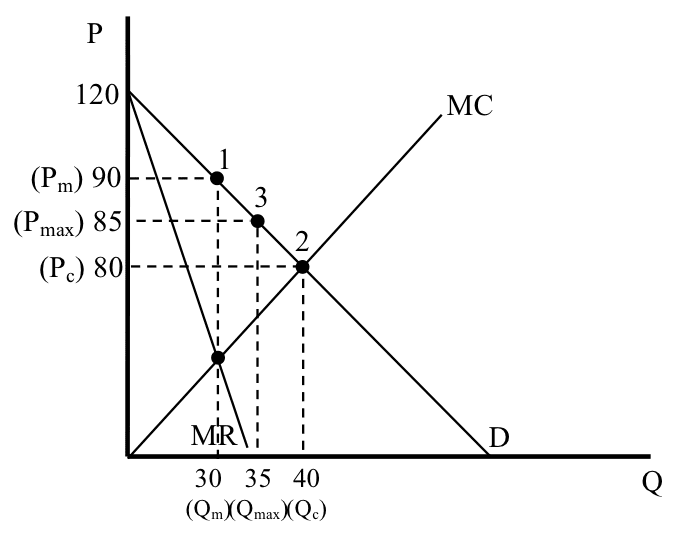
| 1. תמונת המצב ללא התערבות ממשלתית | |
|
כמות הייצור: 30 יחידות (MR=MC) |
`[(120-2Q)=2Q]` |
|
המחיר: 90 ש”ח |
`[120-Q]` |
|
רווחי המונופול: 1700 ש”ח |
`[90*30-(30^2+100)=]`
|
2. תמונת המצב בשוק תחרותי |
|
|
כמות הייצור: 40 יחידות (P=MC) |
`[(120-2Q)=2Q]` |
|
המחיר: 80 ש”ח |
`[120-Q]` |
|
רווח היצרנים: 1500 ש”ח |
`[80*40-(40^2+100)=]` |
| 3. תמונת המצב כאשר `P_(MAX)=85` (תרחיש ב') `P_c<P_(MAX)<P_m` | |
|
כמות הייצור: 35 יחידות |
`[120-85=Q]` פונקציית הביקוש |
|
המחיר: 85 ש”ח |
נתון |
|
רווחי המונופול: 1650 ש”ח |
`[85*35-(35^2+100)=]` |
| 4. תמונת המצב כאשר `80=P_(MAX` (תרחיש ג') `P_c=P_(MAX` | |
|
כמות הייצור: 40 יחידות |
`[120-85=Q]` פונקציית הביקוש |
|
המחיר: 80 ש”ח |
נתון |
|
רווחי המונופול: 1500 ש”ח |
`[80*40-(40^2+100)=]` |
מתן סובסידיה ליחידה מיוצרת והטלת מס כולל
מתן סובסידיה בגובה S ש”ח ליחידה מיוצרת, מקטינה את העלות הכוללת של המונופול ב- S*Q ש”ח, וכתוצאה מכך הוא ייצר יותר יחידות.
נראה כמה יחידות ייצר המונופול מדוגמא 1 אם יקבל סובסידיה בגובה 8 ש”ח לכל יחידה מיוצרת.
פונקציית העלות הכוללת היא: `TC =Q^2=100` .
בעקבות מתן הסובסידיה תשתנה פונקציית העלות ל: `TC =Q^2+100-8Q` .
העלות השולית היא: `MC=2Q-8` .
נבחן את השפעת הסובסידיה באמצעות דוגמא 2, המתבססת על נתוני דוגמא 1 בתוספת הסובסידיה.
דוגמא 2
|
נתוני הדוגמא: |
|
|
פונקצית העלות של המונופול: |
`TC=Q^2+100-8*Q` |
|
פונקצית הביקוש בשוק: |
`P=120-Q` |
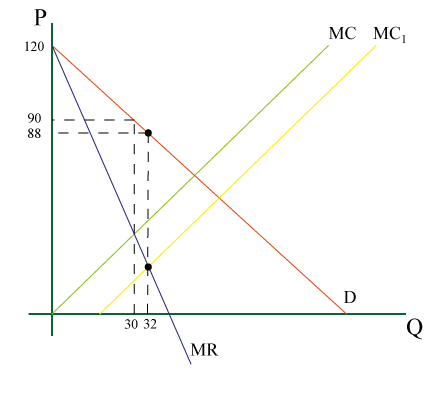
הפתרון (בליווי תרשים 25)
כמות הייצור: 32 יחידות `[MR=MC]->([120-2Q]=[2Q-8])` (לעומת 30 יח' ללא סובסידיה)
המחיר: 88 ש”ח `(P=120-32)` (לעומת 90 ש”ח ללא סובסידיה)
תרשים 25
מציאת הסובסידיה ליחידה הדרושה לייצור כמות מטרה כלשהי
נניח שאנו רוצים לגרום למונופול לייצר את הכמות שהייתה מתקבלת בשוק תחרותי.
בעזרת דוגמא 3, שמתייחסת לנתוני דוגמא 1, נחשב מהי הסובסידיה הנדרשת ליחידה כדי שהמונופול ייצר כמות של 40 יחידות, שהיא הכמות שהייתה מתקבלת בשוק תחרותי.
דוגמא 3
|
נתוני הדוגמא: |
|
|
|
פונקצית העלות של המונופול: |
`TC = Q^2+100-SQ` |
S– סכום הסובסדיה ליח' |
|
פונקצית הביקוש בשוק: |
`P=120-Q` |
|
נחשב את הסובסידיה הדרושה למונופול כדי לייצר 40 יחידות, שהיא הכמות המתקבלת בשוק תחרותי.
הפתרון
נחשב את הנתונים הבאים:
|
הנתונים |
התוצאה |
הסברים ופרשנות |
||
|
MC (כאשר Q = 40) |
[80-S] ש”ח |
|
||
|
MR (כאשר Q = 40) |
40 ש”ח |
|
||
|
S (גובה הסובסידיה) |
40 ש”ח |
צריך להתקיים השוויון `MR=MC:quad[80-S]=40` |
||
|
המחיר בשוק |
80 ש”ח |
|
||
|
רווח המונופול |
3100 ש”ח |
`Pi=[40*80]-[(40)^2+100-(40*40)]` |
מסקנה
אילולא הסובסידיה, רווחי המונופול היו מסתכמים ב- 1700 ש”ח (דוגמא 1 סעיף 1). בעקבות הסובסידיה רווחיו יגדלו.
הטלת מס גלובלי על המונופול
הממשלה יכולה להטיל על המונופול מס גלובלי בסכום הסובסידיה, או בכל סכום אחר, וכך תחזיר לעצמה את סכום הסובסידיה, או כל סכום אחר שתקבע.
התייחסות לסובסידיה ולמס גלובלי
נתייחס לנתוני דוגמא 3 בתוספת מס גלובלי בסך 1600 ש”ח.
הסובסידיה ליחידה היא בגובה 40 ש”ח.
הסובסידיה ליחידה והמס הגלובלי מקבלים ביטוי בפונקציית TC כדלקמן:
`TC = Q^2+100-40Q+1600`
כשנגזור את TC נקבל: `MC=2Q-40`
לאחר הגזירה, המס הגלובלי נעלם, ואילו סכום הסובסידיה ליחידה נשאר. כתוצאה מכך הסובסידיה משפיעה על החלטת המונופול כמה לייצר, ואילו המס הגלובלי לא משפיע.
המס הגלובלי הוא למעשה הוצאה קבועה ולפיכך אינו נכלל בהוצאה השולית.
המס הגלובלי משפיע על הרווח הכולל של המונופול, ועל ההחלטה של המונופול אם בכלל לייצר. אם המס יגרום לו הפסד, המונופול יפסיק את הייצור מיד.