שאלה 9
חברת X חילקה אתמול דיבידנד בגובה 5$ למניה. ב- 7 השנים הבאות הרווחים יגדלו בקצב של 10% לשנה. לאחר מכן יתייצב הגידול ל- 8% לשנה לנצח.
בהנחה שהחברה מחלקת את כל הרווחים כדיבידנד, מהו מחיר המניה, אם מחיר ההון הוא 13%?
תשובה
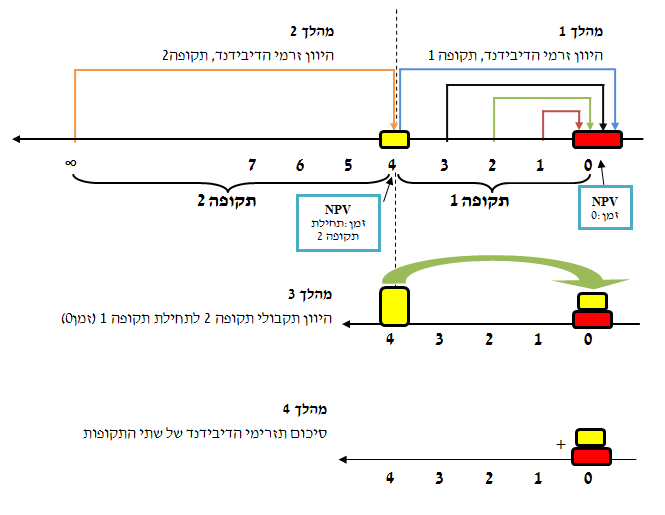
הצגה גרפית של 4 מהלכי הפתרון
מהלך 1
חישוב NPV של תזרימי הדיבידנד בתקופה 1 (7 השנים הראשונות).
NPV מתייחס לזמן 0.
התזרים מוצג בטבלת התזרים של תקופה 1.
מועד 0 מתייחס לרגע שלאחר תשלום הדיבידנד האחרון.
טבלת התזרים של תקופה 1
|
מועדים |
סכומים |
פירוט החישוב |
|
0 |
– |
|
|
1 |
5.5 ש”ח |
$5*(1.1)1 = |
|
2 |
6.05 ש”ח |
$5*(1.1)2 = |
|
3 |
6.655 ש”ח |
$5*(1.1)3 = |
|
4 |
7.320 ש”ח |
$5*(1.1)4 = |
|
5 |
8.052 ש”ח |
$5*(1.1)5 = |
|
6 |
8.857 ש”ח |
$5*(1.1)6 = |
|
7 |
9.743 ש”ח |
$5*(1.1)7 = |
חישוב בעזרת מחשבון
I. מצב המחשבון Cash + d.editor
II. סדר הפעולות
|
|
סימולים ומקשים |
הקלדה |
|
1. |
i% |
13 |
|
2. |
(מועד 0) 1 |
0 |
|
3. |
(” 1) 2 |
5.5 |
|
4. |
(” 2) 3 |
6.05 |
|
5. |
(” 3) 4 |
6.655 |
|
6. |
(” 4) 5 |
7.320 |
|
7. |
(” 5) 6 |
8.052 |
|
8. |
(” 6) 7 |
8.857 |
|
9. |
(” 7) 8 |
9.743 |
|
10. |
ESC |
|
|
11. |
NPV + SOLVE |
|
|
התוצאה: |
NPV = |
31.472 |
התוצאה: NPV = 31.472
מהלך 2
חישוב NPV של תזרימי הדיבידנד בתקופה 2 (מסוף השנה השמינית ולנצח). ה- NPV מתייחס לתחילת התקופה השניה.
הנוסחה הרלוונטית לחישוב NPV של תזרימי דיבידנד שצומחים ב- g% לשנה ולנצח היא: `(D_0*(1+g))/(K_e-g)`.
כאשר: D0 מסמל את תשלום הדיבידנד האחרון (שלפני תקופת חישוב ה- NPV) ו- Ke מסמל את מחיר ההון.
בנתוני השאלה:
והתוצאה:$210.4
מהלך 3
מהלך 4
שאלה 13
נתונה איגרת חוב בעלת ערך נקוב של 100 ש”ח וריבית שנתית נקובה בשיעור של 10% למשך 4 שנים (משולמת כל סוף תקופה).
אם שיעור התשואה לפדיון של איגרת החוב הינו 20% מהו מחיר האיגרת?
תשובה
מלא את הנתונים החסרים וחשב
נתוני האג”ח: ע.נ: 100 ש”ח, ז”פ ______ שנים, קופונים 1 * %_______
נתוני השוק: מחיר ההון: 20%.
טבלת התזרים (מלא בעצמך)
|
מועדים |
סכומים |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
חשב בעזרת מחשבון את NPV של התזרים.
I. מצב המחשבון ____?____
II. סדר הפעולות – מלא בעצמך
|
|
|
סימולים ומקשים |
הקלדה |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
NPV + SOLVE |
|
|
|
התוצאה: NPV = |
___?____ |
|
שאלה 17
בנק מציע הלוואה בסך 5 מיליון ש”ח בתשלומים שנתיים שווים של קרן וריבית. הריבית על החוב לשנה הינה 5.4% והתקופה לפירעון החוב הינה 10 שנים.
מהו התשלום התקופתי?
תשובה
פתרון
תחילה נכין את טבלת התזרים.
מקרא
PMT – תשלום (קיצור של Payment)
טבלת התזרים
|
מועדים |
סכומים |
הערות ופרשנות |
|
0 |
5,000,000$ |
קבלת ההלוואה |
|
1 |
–PMT |
סכום ההחזר השנתי אינו ידוע |
|
2 |
|
|
|
…. |
|
|
|
10 |
PMT- |
|
חישוב בעזרת מחשבון
I. מצב המחשבון CMPD
II. סדר הפעולות
|
|
סימולים ומקשים |
הקלדה |
|
1. |
n |
10 |
|
2. |
i |
5.4% |
|
3. |
PV |
5,000,000 |
|
4. |
PMT + SOLVE |
|
|
התוצאה PMT = |
660,160.77- |
|